|
| 1 | +# 1937. Maximum Number of Points with Cost |
| 2 | + |
| 3 | +- Difficulty: Medium. |
| 4 | +- Related Topics: Array, Dynamic Programming. |
| 5 | +- Similar Questions: Minimum Path Sum, Minimize the Difference Between Target and Chosen Elements. |
| 6 | + |
| 7 | +## Problem |
| 8 | + |
| 9 | +You are given an `m x n` integer matrix `points` (**0-indexed**). Starting with `0` points, you want to **maximize** the number of points you can get from the matrix. |
| 10 | + |
| 11 | +To gain points, you must pick one cell in **each row**. Picking the cell at coordinates `(r, c)` will **add** `points[r][c]` to your score. |
| 12 | + |
| 13 | +However, you will lose points if you pick a cell too far from the cell that you picked in the previous row. For every two adjacent rows `r` and `r + 1` (where `0 <= r < m - 1`), picking cells at coordinates `(r, c1)` and `(r + 1, c2)` will **subtract** `abs(c1 - c2)` from your score. |
| 14 | + |
| 15 | +Return **the **maximum** number of points you can achieve**. |
| 16 | + |
| 17 | +`abs(x)` is defined as: |
| 18 | + |
| 19 | + |
| 20 | + |
| 21 | +- `x` for `x >= 0`. |
| 22 | + |
| 23 | +- `-x` for `x < 0`. |
| 24 | + |
| 25 | + |
| 26 | + |
| 27 | +Example 1:** ** |
| 28 | + |
| 29 | +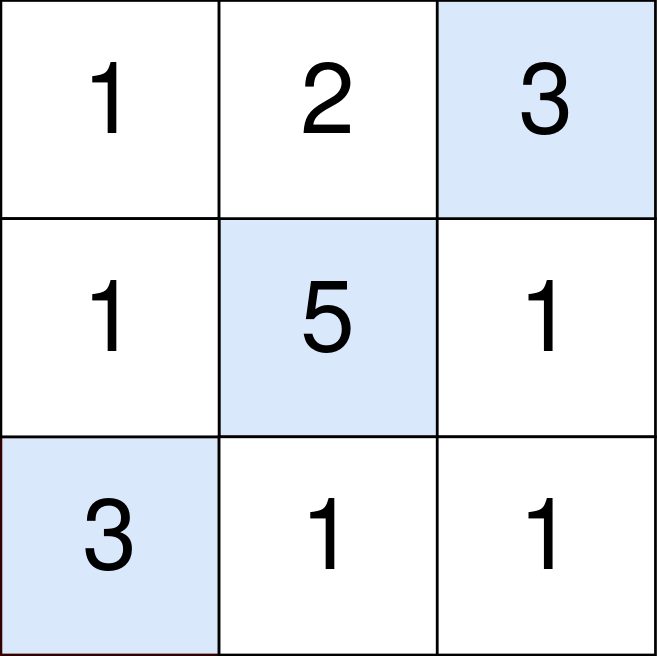 |
| 30 | + |
| 31 | +``` |
| 32 | +Input: points = [[1,2,3],[1,5,1],[3,1,1]] |
| 33 | +Output: 9 |
| 34 | +Explanation: |
| 35 | +The blue cells denote the optimal cells to pick, which have coordinates (0, 2), (1, 1), and (2, 0). |
| 36 | +You add 3 + 5 + 3 = 11 to your score. |
| 37 | +However, you must subtract abs(2 - 1) + abs(1 - 0) = 2 from your score. |
| 38 | +Your final score is 11 - 2 = 9. |
| 39 | +``` |
| 40 | + |
| 41 | +Example 2: |
| 42 | + |
| 43 | +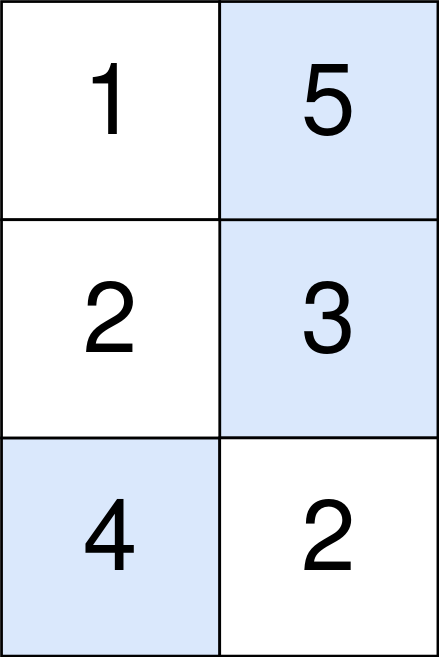 |
| 44 | + |
| 45 | +``` |
| 46 | +Input: points = [[1,5],[2,3],[4,2]] |
| 47 | +Output: 11 |
| 48 | +Explanation: |
| 49 | +The blue cells denote the optimal cells to pick, which have coordinates (0, 1), (1, 1), and (2, 0). |
| 50 | +You add 5 + 3 + 4 = 12 to your score. |
| 51 | +However, you must subtract abs(1 - 1) + abs(1 - 0) = 1 from your score. |
| 52 | +Your final score is 12 - 1 = 11. |
| 53 | +``` |
| 54 | + |
| 55 | + |
| 56 | +**Constraints:** |
| 57 | + |
| 58 | + |
| 59 | + |
| 60 | +- `m == points.length` |
| 61 | + |
| 62 | +- `n == points[r].length` |
| 63 | + |
| 64 | +- `1 <= m, n <= 105` |
| 65 | + |
| 66 | +- `1 <= m * n <= 105` |
| 67 | + |
| 68 | +- `0 <= points[r][c] <= 105` |
| 69 | + |
| 70 | + |
| 71 | + |
| 72 | +## Solution |
| 73 | + |
| 74 | +```javascript |
| 75 | +/** |
| 76 | + * @param {number[][]} points |
| 77 | + * @return {number} |
| 78 | + */ |
| 79 | +var maxPoints = function(points) { |
| 80 | + var m = points.length; |
| 81 | + var n = points[0].length; |
| 82 | + var maxArr = points[m - 1]; |
| 83 | + for (var i = m - 2; i >= 0; i--) { |
| 84 | + var [prefixMaxArr, suffixMaxArr] = getMaxArr(maxArr); |
| 85 | + for (var j = 0; j < n; j++) { |
| 86 | + maxArr[j] = points[i][j] + Math.max(prefixMaxArr[j] - j, suffixMaxArr[j] + j); |
| 87 | + } |
| 88 | + } |
| 89 | + return Math.max(...maxArr); |
| 90 | +}; |
| 91 | + |
| 92 | +var getMaxArr = function(arr) { |
| 93 | + var prefixMaxArr = Array(arr.length); |
| 94 | + var max = Number.MIN_SAFE_INTEGER; |
| 95 | + for (var i = 0; i < arr.length; i++) { |
| 96 | + max = Math.max(max, arr[i] + i); |
| 97 | + prefixMaxArr[i] = max; |
| 98 | + } |
| 99 | + var suffixMaxArr = Array(arr.length); |
| 100 | + max = Number.MIN_SAFE_INTEGER; |
| 101 | + for (var i = arr.length - 1; i >= 0; i--) { |
| 102 | + max = Math.max(max, arr[i] - i); |
| 103 | + suffixMaxArr[i] = max; |
| 104 | + } |
| 105 | + return [prefixMaxArr, suffixMaxArr]; |
| 106 | +}; |
| 107 | +``` |
| 108 | + |
| 109 | +**Explain:** |
| 110 | + |
| 111 | +nope. |
| 112 | + |
| 113 | +**Complexity:** |
| 114 | + |
| 115 | +* Time complexity : O(m * n). |
| 116 | +* Space complexity : O(n). |
0 commit comments