|
| 1 | +# Insertion Sort |
| 2 | + |
| 3 | +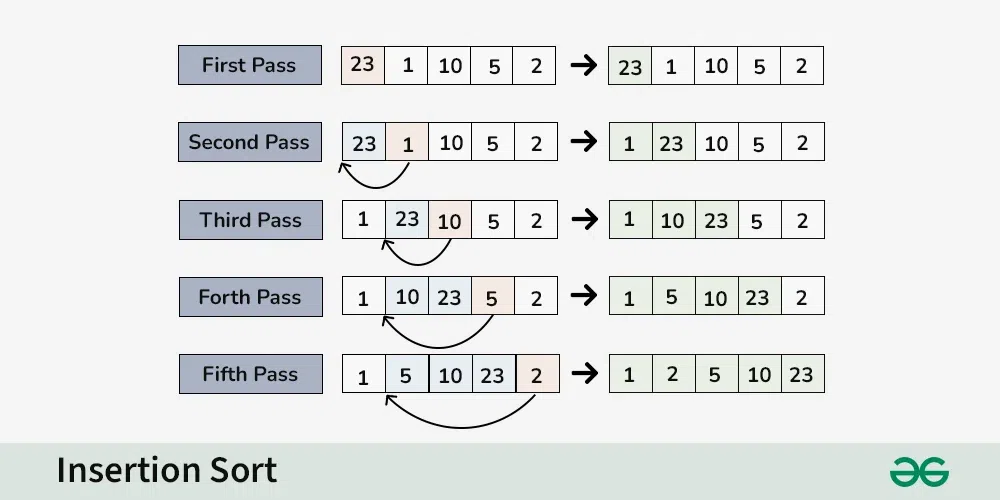 |
| 4 | + |
| 5 | +This repository contains the implementation of **Insertion Sort**, a simple and intuitive sorting algorithm that builds the final sorted array one element at a time. It is particularly efficient for small datasets or partially sorted data. |
| 6 | + |
| 7 | +--- |
| 8 | + |
| 9 | +## Table of Contents |
| 10 | +1. [Introduction](#introduction) |
| 11 | +2. [Algorithm Steps](#algorithm-steps) |
| 12 | +3. [Time and Space Complexity](#time-and-space-complexity) |
| 13 | +4. [Advantages and Disadvantages](#advantages-and-disadvantages) |
| 14 | +5. [Usage](#usage) |
| 15 | +6. [Contact](#contact) |
| 16 | + |
| 17 | +--- |
| 18 | + |
| 19 | +## Introduction |
| 20 | + |
| 21 | +Insertion Sort is a comparison-based sorting algorithm that works by dividing the input into a sorted and an unsorted part. Elements from the unsorted part are picked one at a time and inserted into their correct position in the sorted part. |
| 22 | + |
| 23 | +--- |
| 24 | + |
| 25 | +## Algorithm Steps |
| 26 | + |
| 27 | +1. Start with the second element (index 1), assuming the first element is already sorted. |
| 28 | +2. Compare the current element with the elements in the sorted part of the array. |
| 29 | +3. Shift all larger elements in the sorted part to the right to make room for the current element. |
| 30 | +4. Insert the current element into its correct position. |
| 31 | +5. Repeat until all elements are sorted. |
| 32 | + |
| 33 | +**Example:** |
| 34 | +For an array `[5, 3, 4, 1, 2]`, the algorithm works as follows: |
| 35 | +- Pass 1: `[3, 5, 4, 1, 2]` |
| 36 | +- Pass 2: `[3, 4, 5, 1, 2]` |
| 37 | +- Pass 3: `[1, 3, 4, 5, 2]` |
| 38 | +- Pass 4: `[1, 2, 3, 4, 5]` |
| 39 | + |
| 40 | +--- |
| 41 | + |
| 42 | +## Time and Space Complexity |
| 43 | + |
| 44 | +| Case | Time Complexity | Explanation | |
| 45 | +|---------------|-----------------|------------------------------------------------------| |
| 46 | +| **Best Case** | O(n) | Array is already sorted; only one comparison per element. | |
| 47 | +| **Average Case** | O(n²) | Each element is compared with all previous elements in the worst case. | |
| 48 | +| **Worst Case** | O(n²) | Array is sorted in reverse order; maximum comparisons are needed. | |
| 49 | +| **Space Complexity** | O(1) | In-place sorting algorithm, no additional space is required. | |
| 50 | + |
| 51 | +--- |
| 52 | + |
| 53 | +## Advantages and Disadvantages |
| 54 | + |
| 55 | +### Advantages: |
| 56 | +- Simple and easy to implement. |
| 57 | +- Efficient for small datasets or nearly sorted data. |
| 58 | +- Stable sorting algorithm (preserves the order of equal elements). |
| 59 | + |
| 60 | +### Disadvantages: |
| 61 | +- Inefficient for large datasets due to O(n²) time complexity. |
| 62 | + |
| 63 | +--- |
| 64 | + |
| 65 | +## Usage |
| 66 | + |
| 67 | +To compile and run the code for **Insertion Sort**, use the following commands: |
| 68 | + |
| 69 | +```bash |
| 70 | +# Compile the code |
| 71 | +gcc insertion_sort.c -o insertion_sort |
| 72 | + |
| 73 | +# Run the executable |
| 74 | +./insertion_sort |
0 commit comments