这里我们首先借用一个leetcode上的一道题目来引入哈希表的概念。
我们知道解决这个问题可以使用一个我们之前的Map映射来解决这个问题,保存出现的每一个字符作为键值,出现的次数作为值,创建类似于 Map<Character, Integer> 这样的映射。 使用Map程序实现:
class Solution {
public int firstUniqChar(String s) {
Map<Character, Integer> map = new TreeMap<>();
for(int i = 0; i < s.length(); i++){
char c = s.charAt(i);
map.put(c, map.get(c) == null ? 1: map.get(c) + 1);
}
for(int i = 0; i < s.length(); i++)
if(map.get(s.charAt(i)) == 1)
return i;
return -1;
}
} 可以发现最后运行的效率特别低,所以可以对此进行更改底层实现。在题目的下方标注着:
注意事项:您可以假定该字符串只包含小写字母。
所以说可以使用固定的数组来进行实现。数组大小为 26,数组索引的方式char - 'a'通过这样的方式来找到对应的字符。
使用数组程序实现:
class Solution {
public int firstUniqChar(String s) {
int[] code = new int[26];
for (int i = 0; i < s.length(); i++)
code[s.charAt(i) - 'a']++;
for (int i = 0; i < s.length(); i++)
if (code[s.charAt(i) - 'a'] == 1)
return i;
return -1;
}
} 使用数组(随机访问)实现起来的效率远大于Map的实现效率。char - 'a'就是哈希的哈希函数。哈希表就是将真正关心的内容存储到数组当中,时间复杂度就变成了O(1)级别。
总结: 哈希函数就是将“键”转换为“索引”。而且可以发现我们在哈希表上查找元素的时候时间复杂度为O(1)级别的。所以说我们最后实现的哈希表得时间复杂度为O(1)级别的。在哈希表上的操作难点也就在与如何解决哈希冲突问题上。
哈希函数的设计主要从以下几个方面考虑:
- 一致性:如果a=b,则hash(a) = hash(b),反之不一定成立,对应哈希冲突
- 高效性:计算速度快,简便
- 均匀性:哈希值分布均匀
小范围
- 小范围的正整数可以直接进行使用
- 小范围的负整数可以通过偏移进行归正
大范围 通常的方法是对其进行取模操作,只保留最后的几位,或者具有特征的几位。 但是对于取模的值相对来说是比较讲究的,模值取得越大,相对来说产生哈希冲突的概率越小,具体模值的取值有一个基本规则:
取一个素数(数学领域的范畴,这里不做介绍)
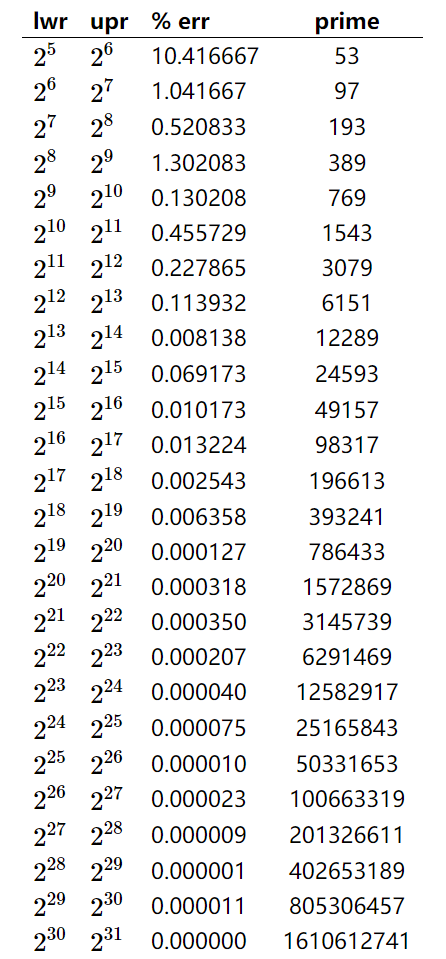
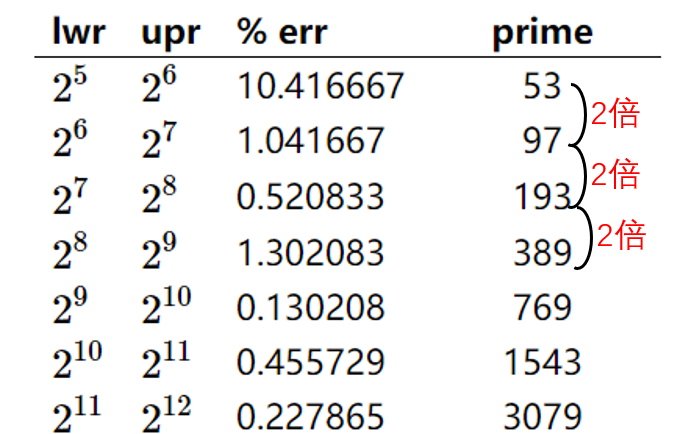
具体素数取什么,有人已经给出了结论。
- lwr:数据大小的下界
- upr:数据大小的上界 也就是数据大小位于(lwr - upr)之间
- err:错误率
- primer:模值的取值(素数)
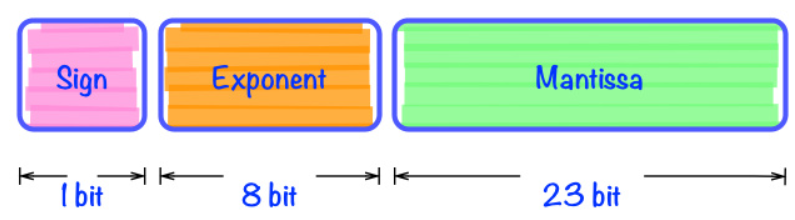
我们知道在我们的计算机当中,对于浮点数的存储也是采用二进制的形式,只不过计算机解析成了浮点数。下面以32位计算机为例。
存储方式同整型相同,所以仍然可以将浮点数按照整型进行处理。
这里字符串依然按照整型进行处理。我们知道整型有下面的变换公式: $$ 2020 = 2 \times 10^3 + 0 \times 10^2 + 2 \times 10^1 + 2 \times 10^0 $$ 字符串依然可以使用这种方式: $$ java = j \times 26^3 + a \times 26^2 + v \times 26^1 + a \times 26^0 $$ 这里我们默认只有小写字母,使用26进制,如果字符串中包含更加复杂的字符,例如大小写,标点符号等等。那么可以使用下面的形式: $$ Java = J \times I^3 + a \times I^2 + v \times I^1 + a \times I^0 $$ I 表示进制,I的数值表示所代表类型的大小。对于字符串产生的这种大整型,我们可以按照2.1节那种,对大整型进行取模。 $$ hash(Java) = (J \times I^3 + a \times I^2 + v \times I^1 + a \times I^0) % M $$ 化简可得: $$ hash(Java) = (((J \times I + a)\times I + v) \times I + a) % M $$
但是上面的式子在不断进行乘法运算的时候,导致在取模之前的数值会变得十分巨大,所以对上面的式子继续进行化简。 $$ hash(Java) = (((J %M \times I + a)%M\times I + v)%M \times I + a) % M $$
根据上面的式子我们可以写出程序实现:
int hash = 0;
for(int i = 0; i < s.length; i++)
hash = (hash * I + s.charAt(i)) % M在Java中的所有类都具有的hasCode()方法,因为hasCode方法在公共基类Object类中,类似于toString()方法。
注意:在Java语言当中hasCode返回类型为int,是允许返回负值的。
当然可以重载hasCode的方法,这样我们在创建类似于HashSet这类底层使用哈希存储的容器类的时候就会调用自己的实现的hasCode方法。 下面以一个Dog类来说明Java里的hasCode();
class Dog{
private String name;
private int age;
private Date birthday;
public Dog(){
name = "WangCai";
age = 4;
birthday = new Date(2020, Calendar.JUNE, 16);
}
@Override
public int hashCode() { //重载hashCode
return name.hashCode() + age + birthday.hashCode();
}
}这样我们在调用 HashSet <Dog> set = new HashSet<>(),就会调用自己的hashCode()进行哈希存储。
根据前面讲解的哈希表的哈希函数,需要对大整型进行取模的操作,其实最后的存储的数据大小就是模值。存储的方式就是采用和动态数组类似的方式,底层采用数组的方式存储。
具体存储到哪个索引的位置就要根据我们的哈希函数设计了。
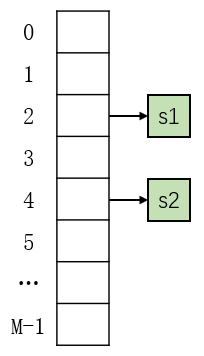
index = ( hashCode(s1) & 0x7fffffff ) % M
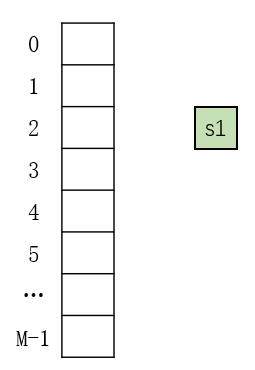
在前面中说到 Java 中的 hasCode 可以返回负值,但是数组索引没有负值,所以需要将最前面的符号位设置为零。 添加两个元素后:
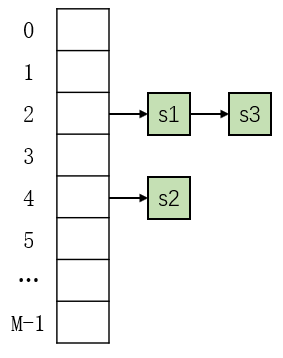
当添加第三个元素(s3)的时候,假设获得的索引依然是 2 。这样就产生了哈希冲突。那么我们就需要将新添加的元素 s3 放到 s1 后面,类似于链表的形式。
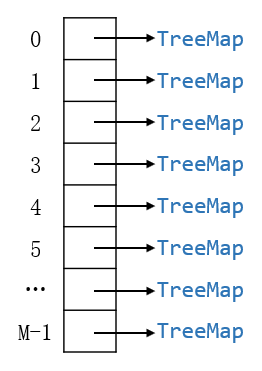
当然前面的形式我们采用链表的形式,其实对于每一个索引位置我们可以索引一个树结构,也就降低了时间复杂度。类似于下面的形式。
实际上HashMap 的底层就是 TreeMap 数组;HashSet 的底层就是 TreeSet 数组;。
这里我们以HashMap的实现为例,我们前面了解到HashMap的底层实现是TreeMap数组,所以我们的类中的变量就必须包含TreeMap数组。
类中的变量主要包含以下几个内容:
- hashTable 数组,里面对应的类型为TreeMap。
- M:对应取模的值,也就是我们数组的大小
- size:用来存储用户数据的大小
public class HashTable<K, V> {
private TreeMap<K, V>[] hashTable;
private int M;
private int size;
public HashTable(int M) {
this.M = M;
size = 0;
hashTable = new TreeMap[M];
for (int i = 0; i < M; i++)
hashTable[i] = new TreeMap<>(); //对每一个TreeMap进行初始化
}
public HashTable(){
this(97);
}
}哈希函数主要是通过获得key的hashCode()进行取模转换后来获得数组索引值。
private int hash(K key) {
return (key.hashCode() & 0x7FFFFFFF) % M;
}所有的基本操作都是首先通过hash(key)获得哈希值进而获得索引值。在通过索引值获得对应索引位置的TreeMap实例。然后对实例进行增删改查操作。 增加元素:
public void add(K key, V value) {
TreeMap<K, V>map = hashTable[hash(key)]; //获得 TreeMap
if (map.containsKey(key))
map.put(key, value);
else{
map.put(key, value);
size++;
}
}
}删除元素:
public V remove(K key) {
TreeMap<K, V> map = hashTable[hash(key)];
if (map.containsKey(key)) {
size--;
return map.remove(key);
}
return null;
}更改元素:
public void set(K key, V value) {
TreeMap<K, V> map = hashTable[hash(key)];
if (map.containsKey(key))
map.put(key, value);
}查找元素:
public boolean contains(K key) {
TreeMap<K, V> map = hashTable[hash(key)];
return map.containsKey(key);
}
public V get(K key) {
return hashTable[hash(key)].get(key);
}最开始的时候我们说过我们在查找的元素时候时间复杂度为O(1)。但是前面的实现经过分析可以得出来,时间复杂度并不为O(1)级别。对于地址为链表的形式,时间复杂度为O(N/M);对于地址为平衡树的形式,时间复杂度为O(log(N/M))。
所以说我们的实现结构还可以进行优化。优化的方式就是动态空间法,类似于之前的动态数组的实现,底层的数组大小是根据用户数据的大小进行动态改变的。
按照之前实现动态数组的方法,引入resize函数,触发resize函数的条件分别有以下两个条件:
- N\M >= upperTol:上界容忍度,触发扩容操作
- N\M <=lowwerTol:下届容忍度,触发缩容操作
下面我们就对上面的实现进行更改。
包含以下几个私有变量:
- capacity: 容量,这是动态更改数组大小的值,全部为素数,取值来源于第2.1节整型。
- upperTol:上界容忍度
- lowerTol:下界容忍度
- capacityIndex:当前capacity的索引值,进而表示当前数组大小
- 其余变量不再做解释
public class HashTable<K, V> { // K不具有可比较性
private final int[] capacity = {
53, 97, 193, 389, 769, 1543, 3079, 6151, 12289, 24593,
49157, 98317, 196613, 393241, 786433, 1572869, 3145739,
6291469,12582917, 25165843, 50331653, 100663319, 201326611,
402653189, 805306457, 1610612741
};
private static final int upperTol = 10;
private static final int lowerTol = 2;
private int capacityIndex = 0;
private TreeMap<K, V>[] hashTable;
private int M;
private int size;
public HashTable() {
this.M = capacity[capacityIndex]; //获取当前数组大小
size = 0;
hashTable = new TreeMap[M];
for (int i = 0; i < M; i++)
hashTable[i] = new TreeMap<>();
}
}同动态数组相同,将原来的数组复制到一个新的容器大小的数组中。通过遍历就哈希表中的所有数据,重新添加到新的哈希表中。
private void resize(int newM) {
TreeMap<K, V>[] newHashTable = new TreeMap[newM];
for (int i = 0; i < newM; i++)
newHashTable[i] = new TreeMap<>();
int oldM = this.M;
this.M = newM; //必须进行更新,后面用到hash()建立在新的M上
for (int i = 0; i < oldM; i++) { //遍历哈希表中所有元素
TreeMap<K, V> map = hashTable[i];
for (K key : map.keySet())
newHashTable[hash(key)].put(key, map.get(key));
}
this.hashTable = newHashTable;
}由于导致数据变化的只有增删操作,对于更改和查询操作并不涉及,具体的更改只需要添加两行代码分别在增删操作上。 增加操作:
if (size >= upperTol * M && capacityIndex + 1 < capacity.length)
resize(capacity[++capacityIndex]);删除操作:
if (size < lowerTol * M && capacityIndex >= 1)
resize(capacity[--capacityIndex]);我们假设数组大小为 M,用户存储的数组为 N。对应着每个地址所存储的元素个数 N / M(平均来说)。
| 类型 | 时间复杂度 |
|---|---|
| 地址为链表 | O(N/M) |
| 地址为平衡树 | O(log(N/M)) |
下面主要是分析地址为平衡树的情况。 首先分析未发生扩容和缩容的过程: 对于增删改查四种操作时间复杂度都是O(log(N/M))级别的。但是我们设置了upperTol和lowerTol。lowerTol <= N\M <= upperTol。两者都是自己设置的常数,所以说时间复杂度均是常数,都是O(1)级别的。 再分析发生扩容的情况: 当我们进行resize操作以后,我们可以发现,oldM 和 newM 之间大约有两倍的关系。
对于原本元素个数为 upperTol * oldM = N 的元素增加到 upperTol * newM = 2 * N,才触发一次resize操作,相当于进行了翻倍操作。resize的时间复杂度为O(N)级别的,但是需要增加N个元素才触发一次resize操作,所以根据均摊时间复杂度,增删两种操作的时间复杂度为O(2)级别的复杂度,改查操作的时间复杂度为O(1)级别。
综上所述: 增加动态空间处理后,所有操作的时间复杂度均为O(1)级别。下面列一个详细的表格:
| 操作 | 详细时间复杂度 | 总时间复杂度 |
|---|---|---|
| 增删操作(前提:未扩容缩容) | O(lowerTol)~O(upperTol) | O(1) |
| 增删操作 | O(lowerTol)~O(upperTol) + O(1) | O(1) |
| 改查操作 | O(1) | O(1) |
更多精彩内容,大家可以转到我的主页:曲怪曲怪的主页
或者关注我的微信公众号:TeaUrn
或者扫描下方二维码进行关注。里面有惊喜等你哦。
源码地址:可在公众号内回复 数据结构与算法源码 即可获得。