-
Notifications
You must be signed in to change notification settings - Fork 254
Find if Path Exists in Graph
- 🔗 Leetcode Link: Find if Path Exists in Graph
- 💡 Problem Difficulty: Easy
- ⏰ Time to complete: 20 mins
- 🛠️ Topics: Graph
- 🗒️ Similar Questions: Find the Town Judge, Find Center of Star Graph
Understand what the interviewer is asking for by using test cases and questions about the problem.
- Established a set (2-3) of test cases to verify their own solution later.
- Established a set (1-2) of edge cases to verify their solution handles complexities.
- Have fully understood the problem and have no clarifying questions.
- Have you verified any Time/Space Constraints for this problem?
- Does the graph have to a connected graph?
- Yes, this graph does not need to be a connected graph.
- How many vertices could there be?
- between 1 and 10000
- Are all edges are unique, there are no duplicate edges correct?
- Yes
- What is the time and space constraints for this problem?
- Let's go with
O(V + E)time andO(V + E)space.
- Let's go with
HAPPY CASE
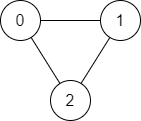
Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
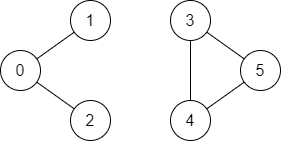
- 0 → 2Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.EDGE CASE
Input: n = 1, edges = [], source = 0, destination = 0
Output: trueMatch what this problem looks like to known categories of problems, e.g. Linked List or Dynamic Programming, and strategies or patterns in those categories.
For Graph Problems, common solution patterns include:
- DFS/BFS: We could use either BFS or DFS. DFS is fewer lines of code, but BFS makes use of the adjacency dictionary data structure.
- Adjacency List: We already have an adjacency list, let's make it a adjacency dictionary.
- Adjacency Matrix: We can use an adjacency matrix to store the graph, but this will make the problem more complicated.
- Topological Sort: In order to have a topological sorting, the graph must not contain any cycles. We cannot apply this sort to this problem because we can have cycles in our graph.
- Union Find: Are there find and union operations here? Can you perform a find operation where you can determine which subset a particular element is in? This can be used for determining if two elements are in the same subset. Can you perform a union operation where you join two subsets into a single subset? Can you check if the two subsets belong to same set? If no, then we cannot perform union.
Plan the solution with appropriate visualizations and pseudocode.
Approach #1 DFS:
General Idea: Let's run a DFS from the source vertex, if we encounter the destination vertex, then we found it.
1. Create an adjacency dictionary to hold the graph, vertex to edges
2. Create a DFS call to visit neighboring vertex
a. Do not continue DFS if vertex was visited or destination was visited
b. Add current vertex to visited set to not revisit visited vertex(avoid infinite loop)
c. Visit vertex neighbors
4. Create a visited set to not revisit visited vertex
5. Call the DFS call on the source vertex
6. Return whether or not we have visited the destination vertexApproach #2 BFS:
1. Create an adjacency dictionary to hold the graph, vertex to edges
2. Create a visited set to not revisit visited vertex
3. BFS call to visit neighboring vertex
a. If vertex was visited, then try the next vertex in queue
b. We have a matching vertex to destination, return True
c. Add vertex to vistied set to not revisit visited vertex(avoid infinite loop)
d. Add neighbors to queue.
6. We have not visited destination vertex, return False- A adjacency dictionary is very important for us to traverse the graph.
Implement the code to solve the algorithm.
Approach #1 DFS:
class Solution:
def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
# Create an adjacency dictionary to hold the graph, vertex to edges
adjacencyDict = defaultdict(list)
for v, u in edges:
adjacencyDict[v].append(u)
adjacencyDict[u].append(v)
# Create a DFS call to visit neighboring vertex
def dfs(vertex):
# Do not continue DFS if vertex was visited or destination was visited
if vertex in visited or destination in visited:
return
# Add current vertex to visited set to not revisit visited vertex(avoid infinite loop)
visited.add(vertex)
# Visit vertex neighbors
for neigh in adjacencyDict[vertex]:
dfs(neigh)
# Create a visited set to not revisit visited vertex
visited = set()
# Call the DFS call on the source vertex
dfs(source)
# Return whether or not we have visited the destination vertex
return destination in visitedApproach #2 BFS:
class Solution:
def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
# Create an adjacency dictionary to hold the graph, vertex to edges
adjacencyDict = defaultdict(list)
for v, u in edges:
adjacencyDict[v].append(u)
adjacencyDict[u].append(v)
# Create a visited set to not revisit visited vertex
visited = set()
# # BFS call to visit neighboring vertex
queue = [source]
while queue:
vertex = queue.pop(0)
# If vertex was visited, then try the next vertex in queue
if vertex in visited:
continue
# We have a matching vertex to destination, return True
elif vertex == destination:
return True
# Add vertex to vistied set to not revisit visited vertex(avoid infinite loop)
visited.add(vertex)
# Add neighbors to queue
for neigh in adjacencyDict[vertex]:
queue.append(neigh)
# We have not visited destination vertex, return False
return FalseReview the code by running specific example(s) and recording values (watchlist) of your code's variables along the way.
- Trace through your code with an input to check for the expected output
- Catch possible edge cases and off-by-one errors
Evaluate the performance of your algorithm and state any strong/weak or future potential work.
Assume V represents the number of vertices/nodes.
Assume E represents the number of edges
- Time Complexity: O(V+E) We may need to visit each vertex/nodes and their edges.
- Space Complexity: O(V+E) accounting for the use of a adjacency dictionary.