README_CN.md

576. 出界的路径数

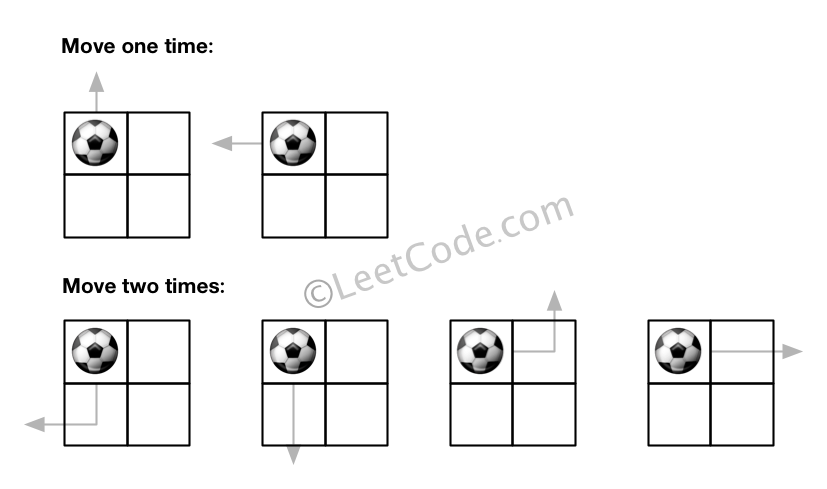
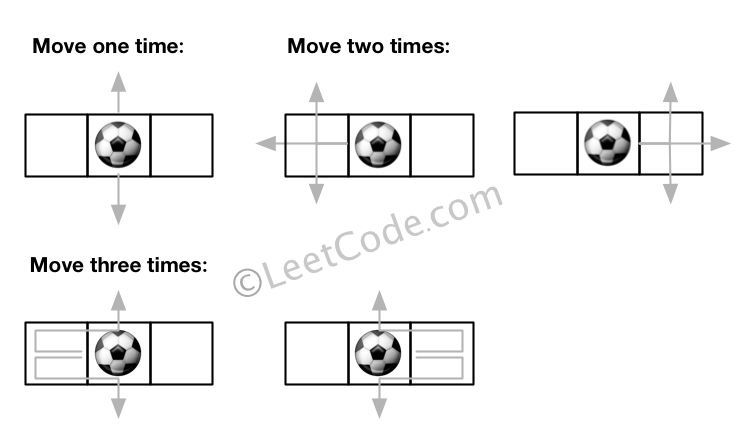
给定一个 m × n 的网格和一个球。球的起始坐标为 (i,j) ，你可以将球移到相邻的单元格内，或者往上、下、左、右四个方向上移动使球穿过网格边界。但是，你最多可以移动 N 次。找出可以将球移出边界的路径数量。答案可能非常大，返回 结果 mod 10⁹ + 7 的值。

示例 1:

输入: m = 2, n = 2, N = 2, i = 0, j = 0
输出: 6
解释: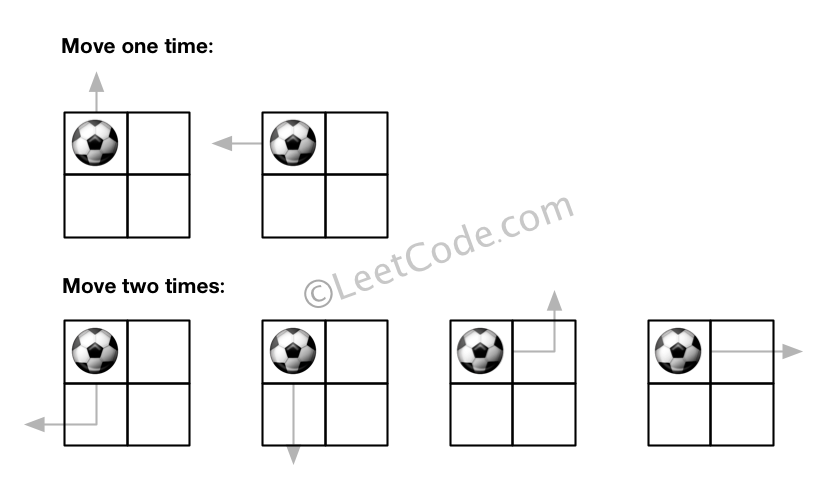

示例 2:

输入: m = 1, n = 3, N = 3, i = 0, j = 1
输出: 12
解释:

说明:

1. 球一旦出界，就不能再被移动回网格内。
2. 网格的长度和高度在 [1,50] 的范围内。
3. N 在 [0,50] 的范围内。

题解 (Rust)

1. 动态规划

impl Solution {
    pub fn find_paths(m: i32, n: i32, max_move: i32, start_row: i32, start_column: i32) -> i32 {
        let mut dp0 = vec![vec![0; n as usize]; m as usize];
        dp0[start_row as usize][start_column as usize] = 1;
        let mut ret = 0;

        for _ in 0..max_move {
            let mut dp1 = vec![vec![0; n as usize]; m as usize];

            for r in 0..m as usize {
                for c in 0..n as usize {
                    if r > 0 {
                        dp1[r - 1][c] = (dp1[r - 1][c] + dp0[r][c]) % 1_000_000_007;
                    } else {
                        ret = (ret + dp0[r][c]) % 1_000_000_007;
                    }
                    if c > 0 {
                        dp1[r][c - 1] = (dp1[r][c - 1] + dp0[r][c]) % 1_000_000_007;
                    } else {
                        ret = (ret + dp0[r][c]) % 1_000_000_007;
                    }
                    if r + 1 < m as usize {
                        dp1[r + 1][c] = (dp1[r + 1][c] + dp0[r][c]) % 1_000_000_007;
                    } else {
                        ret = (ret + dp0[r][c]) % 1_000_000_007;
                    }
                    if c + 1 < n as usize {
                        dp1[r][c + 1] = (dp1[r][c + 1] + dp0[r][c]) % 1_000_000_007;
                    } else {
                        ret = (ret + dp0[r][c]) % 1_000_000_007;
                    }
                }
            }

            dp0 = dp1;
        }

        ret
    }
}