README_CN.md

847. 访问所有节点的最短路径

存在一个由 n 个节点组成的无向连通图，图中的节点按从 0 到 n - 1 编号。

给你一个数组 graph 表示这个图。其中，graph[i] 是一个列表，由所有与节点 i 直接相连的节点组成。

返回能够访问所有节点的最短路径的长度。你可以在任一节点开始和停止，也可以多次重访节点，并且可以重用边。

示例 1:

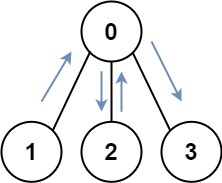
输入: graph = [[1,2,3],[0],[0],[0]]
输出: 4
解释: 一种可能的路径为 [1,0,2,0,3]

示例 2:

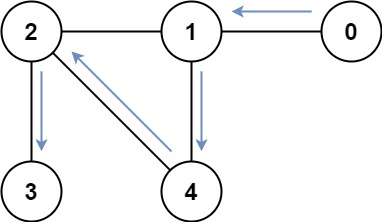
输入: graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
输出: 4
解释: 一种可能的路径为 [0,1,4,2,3]

提示:

• n == graph.length
• 1 <= n <= 12
• 0 <= graph[i].length < n
• graph[i] 不包含 i
• 如果 graph[a] 包含 b ，那么 graph[b] 也包含 a
• 输入的图总是连通图

题解 (Rust)

1. 题解

use std::collections::HashSet;
use std::collections::VecDeque;

impl Solution {
    pub fn shortest_path_length(graph: Vec<Vec<i32>>) -> i32 {
        let n = graph.len() as i32;
        let mut deque = (0..n).map(|i| (i, 1 << i, 0)).collect::<VecDeque<_>>();
        let mut visited = (0..n).map(|i| (i, 1 << i)).collect::<HashSet<_>>();

        while let Some((i, mask, step)) = deque.pop_front() {
            if mask == (1 << n) - 1 {
                return step;
            }

            for &j in &graph[i as usize] {
                if !visited.contains(&(j, mask | (1 << j))) {
                    deque.push_back((j, mask | (1 << j), step + 1));
                    visited.insert((j, mask | (1 << j)));
                }
            }
        }

        unreachable!()
    }
}