README_CN.md

1026. 节点与其祖先之间的最大差值

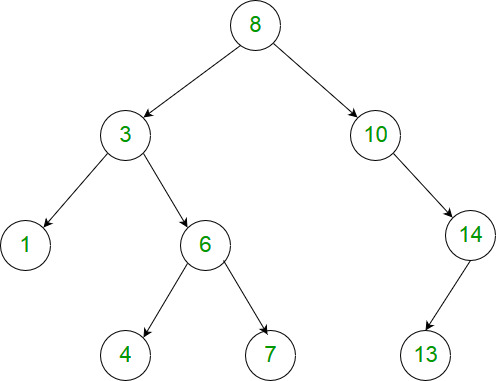
给定二叉树的根节点 root，找出存在于不同节点 A 和 B 之间的最大值 V，其中 V = |A.val - B.val|，且 A 是 B 的祖先。

（如果 A 的任何子节点之一为 B，或者 A 的任何子节点是 B 的祖先，那么我们认为 A 是 B 的祖先）

示例:

输入: [8,3,10,1,6,null,14,null,null,4,7,13]
输出: 7
解释:
我们有大量的节点与其祖先的差值，其中一些如下：
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
在所有可能的差值中，最大值 7 由 |8 - 1| = 7 得出。

提示:

1. 树中的节点数在 2 到 5000 之间。
2. 每个节点的值介于 0 到 100000 之间。

题解 (Python)

1. 递归

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def maxAncestorDiff(self, root: TreeNode) -> int:
        def helper(root: TreeNode) -> (int, int, int):
            if not root:
                return (100001, -1, -1)

            l_min, l_max, l_diff = helper(root.left)
            r_min, r_max, r_diff = helper(root.right)

            lr_min = min(l_min, r_min)
            lr_max = max(l_max, r_max)

            diff = max(l_diff, r_diff)
            if lr_min != 100001:
                diff = max(diff, abs(root.val - lr_min))
            if lr_max != -1:
                diff = max(diff, abs(root.val - lr_max))

            return (min(root.val, lr_min), max(root.val, lr_max), diff)

        return helper(root)[2]