README_CN.md

1105. 填充书架

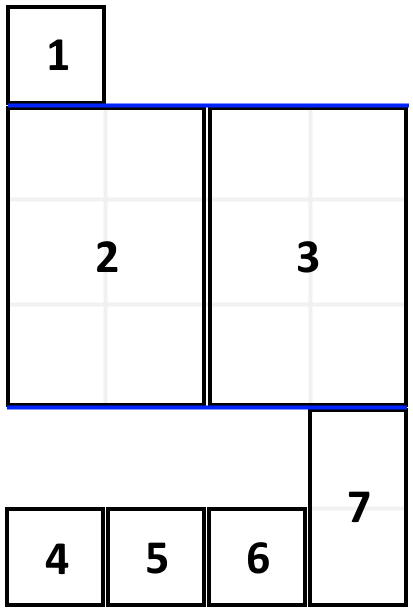
给定一个数组 books ，其中 books[i] = [thicknessi, heighti] 表示第 i 本书的厚度和高度。你也会得到一个整数 shelfWidth 。

按顺序 将这些书摆放到总宽度为 shelfWidth 的书架上。

先选几本书放在书架上（它们的厚度之和小于等于书架的宽度 shelfWidth ），然后再建一层书架。重复这个过程，直到把所有的书都放在书架上。

需要注意的是，在上述过程的每个步骤中，摆放书的顺序与给定图书数组 books 顺序相同。

• 例如，如果这里有 5 本书，那么可能的一种摆放情况是：第一和第二本书放在第一层书架上，第三本书放在第二层书架上，第四和第五本书放在最后一层书架上。

每一层所摆放的书的最大高度就是这一层书架的层高，书架整体的高度为各层高之和。

以这种方式布置书架，返回书架整体可能的最小高度。

示例 1:

输入: books = [[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]], shelfWidth = 4
输出: 6
解释:
3 层书架的高度和为 1 + 3 + 2 = 6 。
第 2 本书不必放在第一层书架上。

示例 2:

输入: books = [[1,3],[2,4],[3,2]], shelfWidth = 6
输出: 4

提示:

• 1 <= books.length <= 1000
• 1 <= thicknessi <= shelfWidth <= 1000
• 1 <= heighti <= 1000

题解 (Rust)

1. 题解

impl Solution {
    pub fn min_height_shelves(books: Vec<Vec<i32>>, shelf_width: i32) -> i32 {
        let mut dp = vec![i32::MAX; books.len() + 1];
        dp[0] = 0;

        for i in 0..dp.len() {
            let mut w = 0;
            let mut h = 0;

            for j in i + 1..dp.len() {
                w += books[j - 1][0];
                h = h.max(books[j - 1][1]);

                if w > shelf_width {
                    break;
                }

                dp[j] = dp[j].min(dp[i] + h);
            }
        }

        *dp.last().unwrap()
    }
}