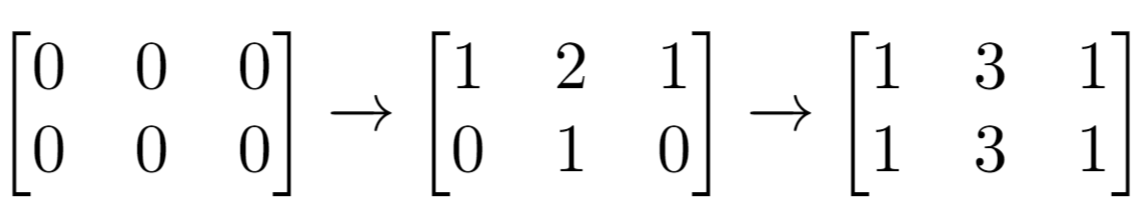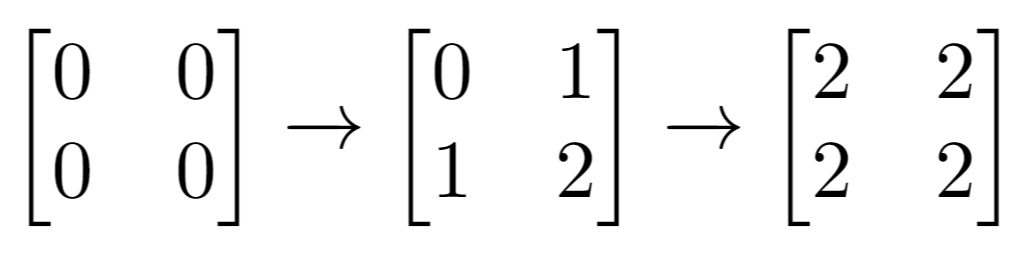README_CN.md

1252. 奇数值单元格的数目

给你一个 n 行 m 列的矩阵，最开始的时候，每个单元格中的值都是 0。

另有一个索引数组 indices，indices[i] = [ri, ci] 中的 ri 和 ci 分别表示指定的行和列（从 0 开始编号）。

你需要将每对 [ri, ci] 指定的行和列上的所有单元格的值加 1。

请你在执行完所有 indices 指定的增量操作后，返回矩阵中 「奇数值单元格」 的数目。

示例 1:

输入: n = 2, m = 3, indices = [[0,1],[1,1]]
输出: 6
解释: 最开始的矩阵是 [[0,0,0],[0,0,0]]。
第一次增量操作后得到 [[1,2,1],[0,1,0]]。
最后的矩阵是 [[1,3,1],[1,3,1]]，里面有 6 个奇数。

示例 2:

输入: n = 2, m = 2, indices = [[1,1],[0,0]]
输出: 0
解释: 最后的矩阵是 [[2,2],[2,2]]，里面没有奇数。

提示:

• 1 <= n <= 50
• 1 <= m <= 50
• 1 <= indices.length <= 100
• 0 <= indices[i][0] < n
• 0 <= indices[i][1] < m

题解 (Rust)

1. 题解

impl Solution {
    pub fn odd_cells(n: i32, m: i32, indices: Vec<Vec<i32>>) -> i32 {
        let mut matrix = vec![vec![false; m as usize]; n as usize];

        for index in indices {
            let ri = index[0] as usize;
            let ci = index[1] as usize;

            for c in 0..(m as usize) {
                matrix[ri][c] = !matrix[ri][c];
            }
            for r in 0..(n as usize) {
                matrix[r][ci] = !matrix[r][ci];
            }
        }

        matrix.iter().map(|r| r.iter().filter(|&&c| c).count() as i32).sum()
    }
}