README_CN.md

1372. 二叉树中的最长交错路径

给你一棵以 root 为根的二叉树，二叉树中的交错路径定义如下：

• 选择二叉树中 任意 节点和一个方向（左或者右）。
• 如果前进方向为右，那么移动到当前节点的的右子节点，否则移动到它的左子节点。
• 改变前进方向：左变右或者右变左。
• 重复第二步和第三步，直到你在树中无法继续移动。

交错路径的长度定义为：访问过的节点数目 - 1（单个节点的路径长度为 0 ）。

请你返回给定树中最长 交错路径 的长度。

示例 1:

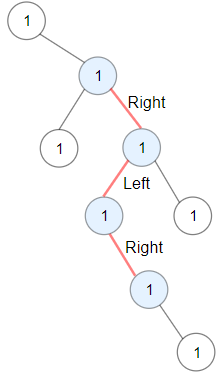
输入: root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1]
输出: 3
解释: 蓝色节点为树中最长交错路径（右 -> 左 -> 右）。

示例 2:

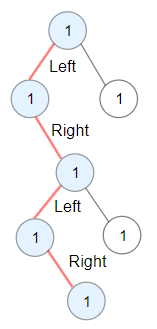
输入: root = [1,1,1,null,1,null,null,1,1,null,1]
输出: 4
解释: 蓝色节点为树中最长交错路径（左 -> 右 -> 左 -> 右）。

示例 3:

输入: root = [1]
输出: 0

提示:

• 每棵树最多有 50000 个节点。
• 每个节点的值在 [1, 100] 之间。

题解 (Python)

1. 题解

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def longestZigZag(self, root: Optional[TreeNode]) -> int:
        return self.dfs(root)[0]

    def dfs(self, root: Optional[TreeNode]) -> (int, int, int):
        if root is None:
            return (0, -1, -1)

        left = self.dfs(root.left)
        right = self.dfs(root.right)
        maxpath = max(left[0], left[1], left[2] + 1,
                      right[0], right[1] + 1, right[2])

        return (maxpath, left[2] + 1, right[1] + 1)