README_CN.md

1643. 第 K 条最小指令

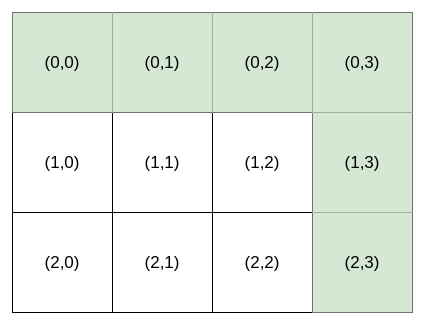
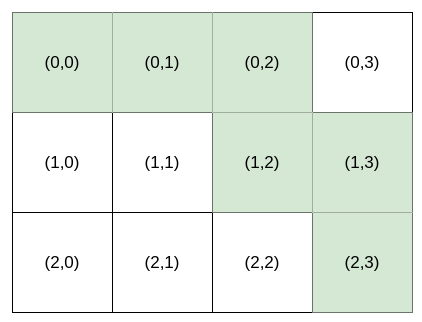
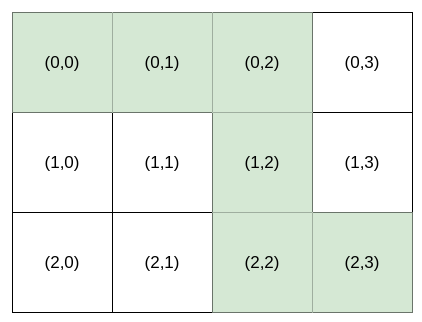
Bob 站在单元格 (0, 0) ，想要前往目的地 destination ：(row, column) 。他只能向 右 或向 下 走。你可以为 Bob 提供导航 指令 来帮助他到达目的地 destination 。

指令 用字符串表示，其中每个字符：

• 'H' ，意味着水平向右移动
• 'V' ，意味着竖直向下移动

能够为 Bob 导航到目的地 destination 的指令可以有多种，例如，如果目的地 destination 是 (2, 3)，"HHHVV" 和 "HVHVH" 都是有效 指令 。

然而，Bob 很挑剔。因为他的幸运数字是 k，他想要遵循 按字典序排列后的第 k 条最小指令 的导航前往目的地 destination 。k 的编号 从 1 开始 。

给你一个整数数组 destination 和一个整数 k ，请你返回可以为 Bob 提供前往目的地 destination 导航的 按字典序排列后的第 k 条最小指令 。

示例 1:

输入: destination = [2,3], k = 1
输出: "HHHVV"
解释: 能前往 (2, 3) 的所有导航指令 按字典序排列后 如下所示：
["HHHVV", "HHVHV", "HHVVH", "HVHHV", "HVHVH", "HVVHH", "VHHHV", "VHHVH", "VHVHH", "VVHHH"].

示例 2:

输入: destination = [2,3], k = 2
输出: "HHVHV"

示例 3:

输入: destination = [2,3], k = 3
输出: "HHVVH"

提示:

• destination.length == 2
• 1 <= row, column <= 15
• 1 <= k <= nCr(row + column, row)，其中 nCr(a, b) 表示组合数，即从 a 个物品中选 b 个物品的不同方案数。

题解 (Rust)

1. 题解

impl Solution {
    pub fn kth_smallest_path(destination: Vec<i32>, k: i32) -> String {
        let row = destination[0] as usize;
        let column = destination[1] as usize;
        let mut k = k as usize;
        let mut dp = vec![vec![1; row + 1]; row + column];
        let mut remainv = row;
        let mut remainh = column;
        let mut instructions = vec![];

        for n in 0..dp.len() {
            for m in 1..dp[0].len().min(n + 1) {
                dp[n][m] = dp[n][m - 1] * (n - m + 1) / m;
            }
        }

        for _ in 0..row + column {
            if remainh > 0 && k <= dp[remainv + remainh - 1][remainv] {
                remainh -= 1;
                instructions.push(b'H');
            } else {
                k -= dp[remainv + remainh - 1][remainv];
                remainv -= 1;
                instructions.push(b'V');
            }
        }

        String::from_utf8(instructions).unwrap()
    }
}