README_CN.md

1901. 寻找峰值 II

一个 2D 网格中的 峰值 是指那些 严格大于 其相邻格子(上、下、左、右)的元素。

给你一个 从 0 开始编号 的 m x n 矩阵 mat ，其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值 mat[i][j] 并 返回其位置 [i,j] 。

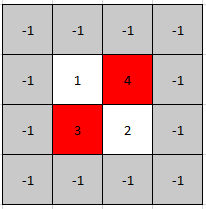
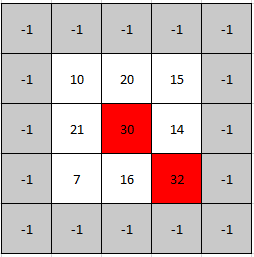
你可以假设整个矩阵周边环绕着一圈值为 -1 的格子。

要求必须写出时间复杂度为 O(m log(n)) 或 O(n log(m)) 的算法

示例 1:

输入: mat = [[1,4],[3,2]]
输出: [0,1]
解释: 3 和 4 都是峰值，所以[1,0]和[0,1]都是可接受的答案。

示例 2:

输入: mat = [[10,20,15],[21,30,14],[7,16,32]]
输出: [1,1]
解释: 30 和 32 都是峰值，所以[1,1]和[2,2]都是可接受的答案。

提示:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 500
• 1 <= mat[i][j] <= 105
• 任意两个相邻元素均不相等.

题解 (Rust)

1. 题解

impl Solution {
    pub fn find_peak_grid(mat: Vec<Vec<i32>>) -> Vec<i32> {
        let mut i = 0;
        let mut j = 0;

        loop {
            let mut peak_i = i;
            let mut peak_j = j;

            if i > 0 && mat[i - 1][j] > mat[peak_i][peak_j] {
                peak_i = i - 1;
                peak_j = j;
            }
            if i < mat.len() - 1 && mat[i + 1][j] > mat[peak_i][peak_j] {
                peak_i = i + 1;
                peak_j = j;
            }
            if j > 0 && mat[i][j - 1] > mat[peak_i][peak_j] {
                peak_i = i;
                peak_j = j - 1;
            }
            if j < mat[0].len() - 1 && mat[i][j + 1] > mat[peak_i][peak_j] {
                peak_i = i;
                peak_j = j + 1;
            }

            if peak_i == i && peak_j == j {
                break;
            }

            i = peak_i;
            j = peak_j;
        }

        vec![i as i32, j as i32]
    }
}