README_CN.md

1905. 统计子岛屿

给你两个 m x n 的二进制矩阵 grid1 和 grid2 ，它们只包含 0 （表示水域）和 1 （表示陆地）。一个 岛屿 是由 四个方向 （水平或者竖直）上相邻的 1 组成的区域。任何矩阵以外的区域都视为水域。

如果 grid2 的一个岛屿，被 grid1 的一个岛屿 完全 包含，也就是说 grid2 中该岛屿的每一个格子都被 grid1 中同一个岛屿完全包含，那么我们称 grid2 中的这个岛屿为 子岛屿 。

请你返回 grid2 中 子岛屿 的 数目 。

示例 1:

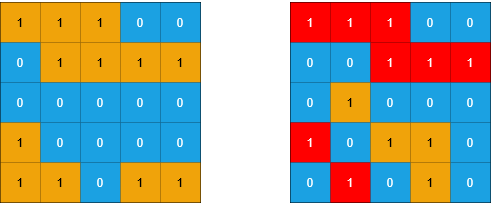
输入: grid1 = [[1,1,1,0,0],[0,1,1,1,1],[0,0,0,0,0],[1,0,0,0,0],[1,1,0,1,1]], grid2 = [[1,1,1,0,0],[0,0,1,1,1],[0,1,0,0,0],[1,0,1,1,0],[0,1,0,1,0]]
输出: 3
解释: 如上图所示，左边为 grid1 ，右边为 grid2 。
grid2 中标红的 1 区域是子岛屿，总共有 3 个子岛屿。

示例 2:

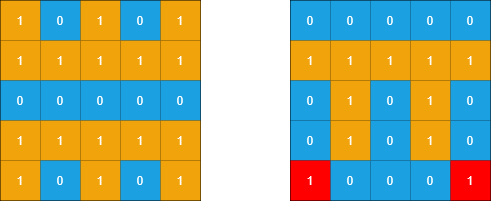
输入: grid1 = [[1,0,1,0,1],[1,1,1,1,1],[0,0,0,0,0],[1,1,1,1,1],[1,0,1,0,1]], grid2 = [[0,0,0,0,0],[1,1,1,1,1],[0,1,0,1,0],[0,1,0,1,0],[1,0,0,0,1]]
输出: 2
解释: 如上图所示，左边为 grid1 ，右边为 grid2 。
grid2 中标红的 1 区域是子岛屿，总共有 2 个子岛屿。

提示:

• m == grid1.length == grid2.length
• n == grid1[i].length == grid2[i].length
• 1 <= m, n <= 500
• grid1[i][j] 和 grid2[i][j] 都要么是 0 要么是 1 。

题解 (Rust)

1. 题解

impl Solution {
    pub fn count_sub_islands(grid1: Vec<Vec<i32>>, grid2: Vec<Vec<i32>>) -> i32 {
        let m = grid1.len();
        let n = grid1[0].len();
        let mut grid2 = grid2;
        let mut ret = 0;

        for i in 0..m {
            for j in 0..n {
                if grid2[i][j] == 0 {
                    continue;
                }

                let mut cells = vec![(i, j)];
                let mut is_sub = true;
                grid2[i][j] = 0;

                while let Some((i, j)) = cells.pop() {
                    is_sub &= grid1[i][j] == 1;

                    if i > 0 && grid2[i - 1][j] == 1 {
                        cells.push((i - 1, j));
                        grid2[i - 1][j] = 0;
                    }
                    if i + 1 < m && grid2[i + 1][j] == 1 {
                        cells.push((i + 1, j));
                        grid2[i + 1][j] = 0;
                    }
                    if j > 0 && grid2[i][j - 1] == 1 {
                        cells.push((i, j - 1));
                        grid2[i][j - 1] = 0;
                    }
                    if j + 1 < n && grid2[i][j + 1] == 1 {
                        cells.push((i, j + 1));
                        grid2[i][j + 1] = 0;
                    }
                }

                ret += is_sub as i32;
            }
        }

        ret
    }
}