README_CN.md

1928. 规定时间内到达终点的最小花费

一个国家有 n 个城市，城市编号为 0 到 n - 1 ，题目保证 所有城市 都由双向道路 连接在一起 。道路由二维整数数组 edges 表示，其中 edges[i] = [xi, yi, timei] 表示城市 xi 和 yi 之间有一条双向道路，耗费时间为 timei 分钟。两个城市之间可能会有多条耗费时间不同的道路，但是不会有道路两头连接着同一座城市。

每次经过一个城市时，你需要付通行费。通行费用一个长度为 n 且下标从 0 开始的整数数组 passingFees 表示，其中 passingFees[j] 是你经过城市 j 需要支付的费用。

一开始，你在城市 0 ，你想要在 maxTime 分钟以内 （包含 maxTime 分钟）到达城市 n - 1 。旅行的 费用 为你经过的所有城市 通行费之和 （包括 起点和终点城市的通行费）。

给你 maxTime，edges 和 passingFees ，请你返回完成旅行的 最小费用 ，如果无法在 maxTime 分钟以内完成旅行，请你返回 -1 。

示例 1:

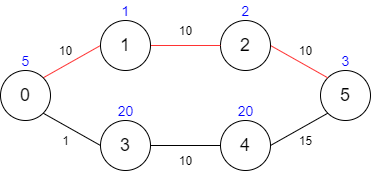
输入: maxTime = 30, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出: 11
解释: 最优路径为 0 -> 1 -> 2 -> 5 ，总共需要耗费 30 分钟，需要支付 11 的通行费。

示例 2:

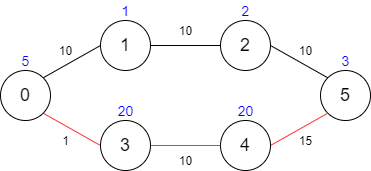
输入: maxTime = 29, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出: 48
解释: 最优路径为 0 -> 3 -> 4 -> 5 ，总共需要耗费 26 分钟，需要支付 48 的通行费。
你不能选择路径 0 -> 1 -> 2 -> 5 ，因为这条路径耗费的时间太长。

示例 3:

输入: maxTime = 25, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出: -1
解释: 无法在 25 分钟以内从城市 0 到达城市 5 。

提示:

• 1 <= maxTime <= 1000
• n == passingFees.length
• 2 <= n <= 1000
• n - 1 <= edges.length <= 1000
• 0 <= xi, yi <= n - 1
• 1 <= timei <= 1000
• 1 <= passingFees[j] <= 1000
• 图中两个节点之间可能有多条路径。
• 图中不含有自环。

题解 (Rust)

1. 题解

impl Solution {
    pub fn min_cost(max_time: i32, edges: Vec<Vec<i32>>, passing_fees: Vec<i32>) -> i32 {
        let max_time = max_time as usize;
        let n = edges.iter().map(|edge| edge[0].max(edge[1])).max().unwrap() as usize + 1;
        let mut dp = vec![vec![i32::MAX; n]; max_time + 1];
        let mut ret = i32::MAX;
        dp[0][0] = passing_fees[0];

        for t in 0..=max_time {
            for edge in &edges {
                let (x, y, time) = (edge[0] as usize, edge[1] as usize, edge[2] as usize);

                if t >= time {
                    if dp[t - time][y] != i32::MAX {
                        dp[t][x] = dp[t][x].min(dp[t - time][y] + passing_fees[x]);
                    }
                    if dp[t - time][x] != i32::MAX {
                        dp[t][y] = dp[t][y].min(dp[t - time][x] + passing_fees[y]);
                    }
                }
            }

            ret = ret.min(dp[t][n - 1]);
        }

        if ret == i32::MAX {
            return -1;
        }

        ret
    }
}