README_CN.md

2101. 引爆最多的炸弹

给你一个炸弹列表。一个炸弹的 爆炸范围 定义为以炸弹为圆心的一个圆。

炸弹用一个下标从 0 开始的二维整数数组 bombs 表示，其中 bombs[i] = [xi, yi, ri] 。xi 和 yi 表示第 i 个炸弹的 X 和 Y 坐标，ri 表示爆炸范围的 半径 。

你需要选择引爆 一个 炸弹。当这个炸弹被引爆时，所有 在它爆炸范围内的炸弹都会被引爆，这些炸弹会进一步将它们爆炸范围内的其他炸弹引爆。

给你数组 bombs ，请你返回在引爆 一个 炸弹的前提下，最多 能引爆的炸弹数目。

示例 1:

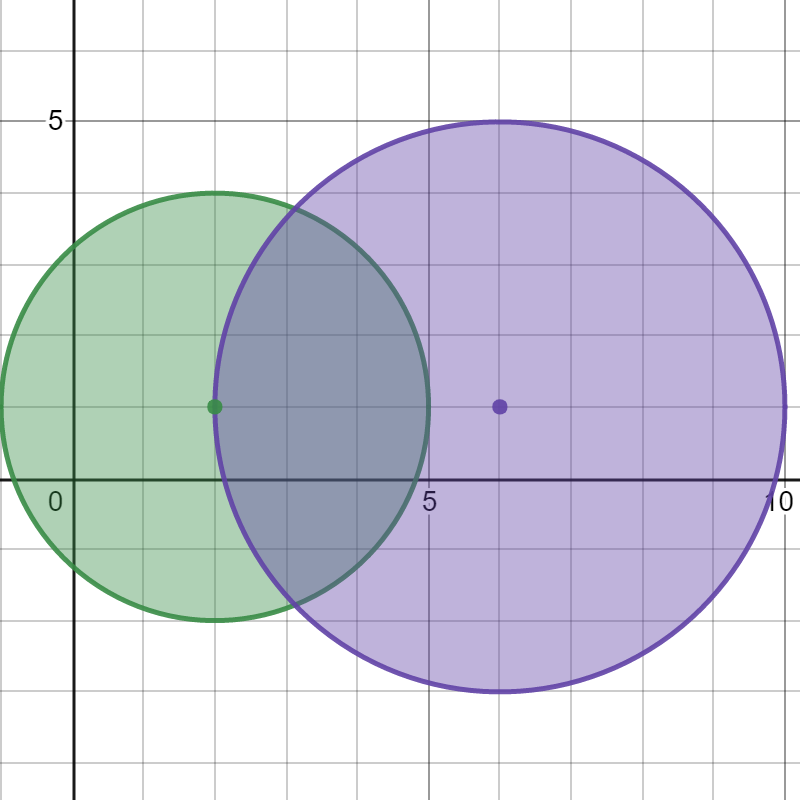
输入: bombs = [[2,1,3],[6,1,4]]
输出: 2
解释:
上图展示了 2 个炸弹的位置和爆炸范围。
如果我们引爆左边的炸弹，右边的炸弹不会被影响。
但如果我们引爆右边的炸弹，两个炸弹都会爆炸。
所以最多能引爆的炸弹数目是 max(1, 2) = 2 。

示例 2:

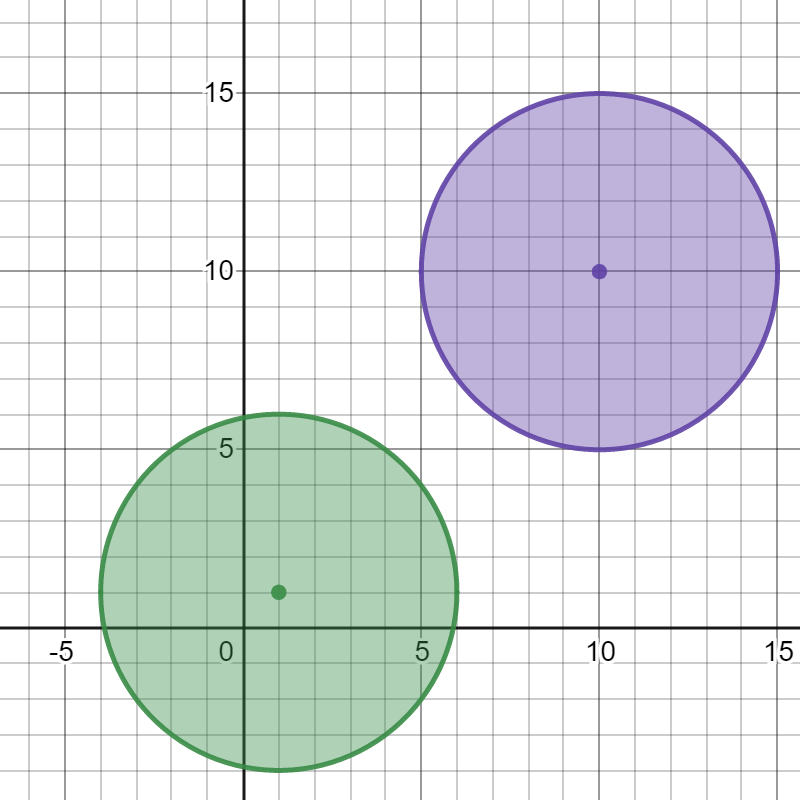
输入: bombs = [[1,1,5],[10,10,5]]
输出: 1
解释:
引爆任意一个炸弹都不会引爆另一个炸弹。所以最多能引爆的炸弹数目为 1 。

示例 3:

输入: bombs = [[1,2,3],[2,3,1],[3,4,2],[4,5,3],[5,6,4]]
输出: 5
解释:
最佳引爆炸弹为炸弹 0 ，因为：
- 炸弹 0 引爆炸弹 1 和 2 。红色圆表示炸弹 0 的爆炸范围。
- 炸弹 2 引爆炸弹 3 。蓝色圆表示炸弹 2 的爆炸范围。
- 炸弹 3 引爆炸弹 4 。绿色圆表示炸弹 3 的爆炸范围。
所以总共有 5 个炸弹被引爆。

提示:

• 1 <= bombs.length <= 100
• bombs[i].length == 3
• 1 <= xi, yi, ri <= 105

题解 (Rust)

1. 题解

use std::collections::HashSet;

impl Solution {
    pub fn maximum_detonation(bombs: Vec<Vec<i32>>) -> i32 {
        let mut edges = vec![vec![]; bombs.len()];
        let mut visited = HashSet::new();
        let mut stack = vec![];
        let mut ret = 0;

        for i in 0..bombs.len() {
            for j in 0..bombs.len() {
                let x2 = ((bombs[i][0] - bombs[j][0]) as i64).pow(2);
                let y2 = ((bombs[i][1] - bombs[j][1]) as i64).pow(2);
                let r2 = (bombs[i][2] as i64).pow(2);

                if x2 + y2 <= r2 {
                    edges[i].push(j);
                }
            }
        }

        for i in 0..bombs.len() {
            visited.clear();
            visited.insert(i);
            stack.clear();
            stack.push(i);

            while let Some(j) = stack.pop() {
                for &k in &edges[j] {
                    if !visited.contains(&k) {
                        visited.insert(k);
                        stack.push(k);
                    }
                }
            }

            ret = ret.max(visited.len());
        }

        ret as i32
    }
}