README_CN.md

2258. 逃离火灾

给你一个下标从 0 开始大小为 m x n 的二维整数数组 grid ，它表示一个网格图。每个格子为下面 3 个值之一：

• 0 表示草地。
• 1 表示着火的格子。
• 2 表示一座墙，你跟火都不能通过这个格子。

一开始你在最左上角的格子 (0, 0) ，你想要到达最右下角的安全屋格子 (m - 1, n - 1) 。每一分钟，你可以移动到 相邻 的草地格子。每次你移动 之后 ，着火的格子会扩散到所有不是墙的 相邻 格子。

请你返回你在初始位置可以停留的 最多 分钟数，且停留完这段时间后你还能安全到达安全屋。如果无法实现，请你返回 -1 。如果不管你在初始位置停留多久，你 总是 能到达安全屋，请你返回 109 。

注意，如果你到达安全屋后，火马上到了安全屋，这视为你能够安全到达安全屋。

如果两个格子有共同边，那么它们为 相邻 格子。

示例 1:

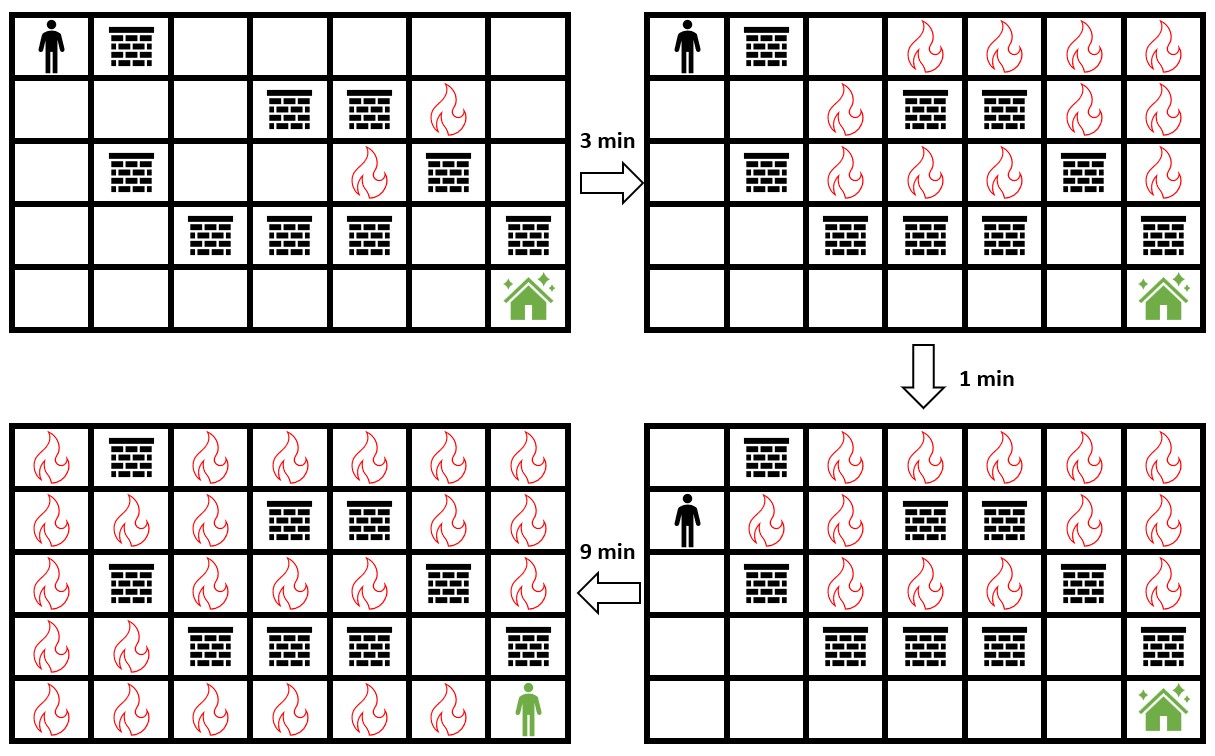
输入: grid = [[0,2,0,0,0,0,0],[0,0,0,2,2,1,0],[0,2,0,0,1,2,0],[0,0,2,2,2,0,2],[0,0,0,0,0,0,0]]
输出: 3
解释: 上图展示了你在初始位置停留 3 分钟后的情形。
你仍然可以安全到达安全屋。
停留超过 3 分钟会让你无法安全到达安全屋。

示例 2:

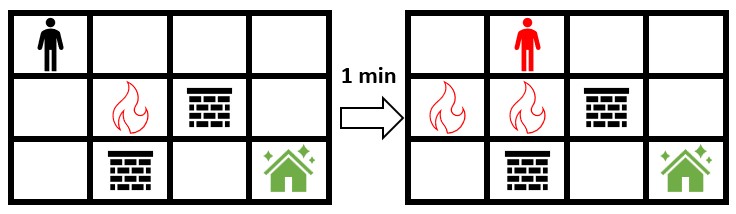
输入: grid = [[0,0,0,0],[0,1,2,0],[0,2,0,0]]
输出: -1
解释: 上图展示了你马上开始朝安全屋移动的情形。
火会蔓延到你可以移动的所有格子，所以无法安全到达安全屋。
所以返回 -1 。

示例 3:

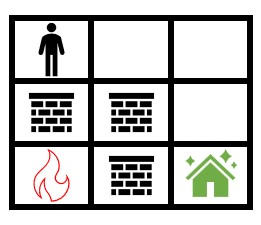
输入: grid = [[0,0,0],[2,2,0],[1,2,0]]
输出: 1000000000
解释: 上图展示了初始网格图。
注意，由于火被墙围了起来，所以无论如何你都能安全到达安全屋。
所以返回 109 。

提示:

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 300
• 4 <= m * n <= 2 * 104
• grid[i][j] 是 0 ，1 或者 2 。
• grid[0][0] == grid[m - 1][n - 1] == 0

题解 (Rust)

1. 题解

use std::collections::VecDeque;

impl Solution {
    fn canReach(
        mut grid: Vec<Vec<i32>>,
        mut fire: VecDeque<(usize, usize, i32)>,
        mut minutes: i32,
    ) -> bool {
        let (m, n) = (grid.len(), grid[0].len());
        let mut person = VecDeque::from([(0, 0, minutes)]);
        grid[0][0] = -1;

        while let Some(&(i, j, t)) = fire.front() {
            if t >= minutes {
                break;
            }

            if i > 0 && grid[i - 1][j] < 1 {
                grid[i - 1][j] = 1;
                fire.push_back((i - 1, j, t + 1));
            }
            if i + 1 < m && grid[i + 1][j] < 1 {
                grid[i + 1][j] = 1;
                fire.push_back((i + 1, j, t + 1));
            }
            if j > 0 && grid[i][j - 1] < 1 {
                grid[i][j - 1] = 1;
                fire.push_back((i, j - 1, t + 1));
            }
            if j + 1 < n && grid[i][j + 1] < 1 {
                grid[i][j + 1] = 1;
                fire.push_back((i, j + 1, t + 1));
            }

            fire.pop_front();
        }

        while !person.is_empty() {
            while let Some(&(i, j, t)) = person.front() {
                if i == m - 1 && j == n - 1 {
                    return true;
                }

                if t > minutes {
                    break;
                }

                if grid[i][j] < 1 {
                    if i > 0 && grid[i - 1][j] == 0 {
                        grid[i - 1][j] = -1;
                        person.push_back((i - 1, j, t + 1));
                    }
                    if i + 1 < m && grid[i + 1][j] == 0 {
                        grid[i + 1][j] = -1;
                        person.push_back((i + 1, j, t + 1));
                    }
                    if j > 0 && grid[i][j - 1] == 0 {
                        grid[i][j - 1] = -1;
                        person.push_back((i, j - 1, t + 1));
                    }
                    if j + 1 < n && grid[i][j + 1] == 0 {
                        grid[i][j + 1] = -1;
                        person.push_back((i, j + 1, t + 1));
                    }
                }

                person.pop_front();
            }

            while let Some(&(i, j, t)) = fire.front() {
                if t > minutes {
                    break;
                }

                if i > 0 && grid[i - 1][j] < 1 {
                    grid[i - 1][j] = 1;
                    fire.push_back((i - 1, j, t + 1));
                }
                if i + 1 < m && grid[i + 1][j] < 1 {
                    grid[i + 1][j] = 1;
                    fire.push_back((i + 1, j, t + 1));
                }
                if j > 0 && grid[i][j - 1] < 1 {
                    grid[i][j - 1] = 1;
                    fire.push_back((i, j - 1, t + 1));
                }
                if j + 1 < n && grid[i][j + 1] < 1 {
                    grid[i][j + 1] = 1;
                    fire.push_back((i, j + 1, t + 1));
                }

                fire.pop_front();
            }

            minutes += 1;
        }

        false
    }
    pub fn maximum_minutes(grid: Vec<Vec<i32>>) -> i32 {
        let (m, n) = (grid.len(), grid[0].len());
        let mut init_fire = VecDeque::new();
        let mut lo = 0;
        let mut hi = (m * n) as i32;

        for i in 0..m {
            for j in 0..n {
                if grid[i][j] == 1 {
                    init_fire.push_back((i, j, 0));
                }
            }
        }

        if !Self::canReach(grid.clone(), init_fire.clone(), lo) {
            return -1;
        }
        if Self::canReach(grid.clone(), init_fire.clone(), hi) {
            return 1_000_000_000;
        }

        while lo < hi {
            let mid = (lo + hi + 1) / 2;

            if Self::canReach(grid.clone(), init_fire.clone(), mid) {
                lo = mid;
            } else {
                hi = mid - 1;
            }
        }

        hi
    }
}