README_CN.md

2498. 青蛙过河 II

给你一个下标从 0 开始的整数数组 stones ，数组中的元素 严格递增 ，表示一条河中石头的位置。

一只青蛙一开始在第一块石头上，它想到达最后一块石头，然后回到第一块石头。同时每块石头 至多 到达 一次。

一次跳跃的 长度 是青蛙跳跃前和跳跃后所在两块石头之间的距离。

• 更正式的，如果青蛙从 stones[i] 跳到 stones[j] ，跳跃的长度为 |stones[i] - stones[j]| 。

一条路径的 代价 是这条路径里的 最大跳跃长度 。

请你返回这只青蛙的 最小代价 。

示例 1:

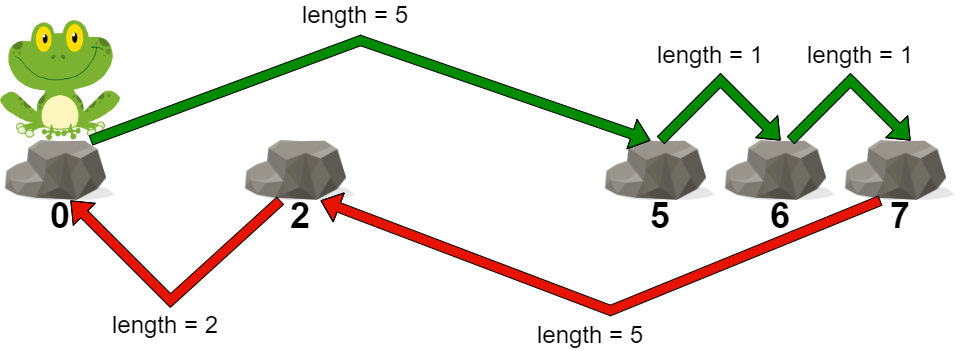
输入: stones = [0,2,5,6,7]
输出: 5
解释: 上图展示了一条最优路径。
这条路径的代价是 5 ，是这条路径中的最大跳跃长度。
无法得到一条代价小于 5 的路径，我们返回 5 。

示例 2:

输入: stones = [0,3,9]
输出: 9
解释:
青蛙可以直接跳到最后一块石头，然后跳回第一块石头。
在这条路径中，每次跳跃长度都是 9 。所以路径代价是 max(9, 9) = 9 。
这是可行路径中的最小代价。

提示:

• 2 <= stones.length <= 105
• 0 <= stones[i] <= 109
• stones[0] == 0
• stones 中的元素严格递增。

题解 (Rust)

1. 题解

impl Solution {
    pub fn max_jump(stones: Vec<i32>) -> i32 {
        let mut lo = 1;
        let mut hi = *stones.last().unwrap();

        while lo < hi {
            let mid = (lo + hi) / 2;
            let mut i = 0;
            let mut j = 1;
            let mut flag = true;
            let mut used = vec![false; stones.len()];

            while i < stones.len() - 1 {
                if stones[j] - stones[j - 1] > mid {
                    flag = false;
                    break;
                } else if j == stones.len() - 1 || stones[j + 1] - stones[i] > mid {
                    i = j;
                    used[i] = true;
                }

                j += 1;
            }

            if flag {
                used[i] = false;
                i = 0;
                j = 1;

                while i < stones.len() - 1 {
                    if stones[j] - stones[i] > mid {
                        flag = false;
                        break;
                    } else if !used[j] && stones[j] - stones[i] <= mid {
                        i = j;
                    }

                    j += 1;
                }
            }

            if flag {
                hi = mid;
            } else {
                lo = mid + 1;
            }
        }

        hi
    }
}