2322. Minimum Score After Removals on a Tree #1964
-
|
Topics: There is an undirected connected tree with n nodes labeled from You are given a 0-indexed integer array Remove two distinct edges of the tree to form three connected components. For a pair of removed edges, the following steps are defined:
Return the minimum score of any possible pair of edge removals on the given tree. Example 1:
Example 2:
Constraints:
Hint:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to find the minimum score after removing two distinct edges from a tree, resulting in three connected components. The score is defined as the difference between the largest and smallest XOR values of the three components. Approach
Let's implement this solution in PHP: 2322. Minimum Score After Removals on a Tree <?php
class Solution {
private $graph;
private $nums;
private $in_time;
private $out_time;
private $parent;
private $subtree_xor;
private $time;
/**
* @param Integer[] $nums
* @param Integer[][] $edges
* @return Integer
*/
function minimumScore($nums, $edges) {
$n = count($nums);
$this->nums = $nums;
$this->graph = array_fill(0, $n, []);
foreach ($edges as $edge) {
$u = $edge[0];
$v = $edge[1];
$this->graph[$u][] = $v;
$this->graph[$v][] = $u;
}
$this->in_time = array_fill(0, $n, 0);
$this->out_time = array_fill(0, $n, 0);
$this->parent = array_fill(0, $n, -1);
$this->subtree_xor = array_fill(0, $n, 0);
$this->time = 0;
$this->dfs(0, -1);
$total = $this->subtree_xor[0];
$min_score = PHP_INT_MAX;
for ($v = 1; $v < $n; $v++) {
$T1 = $this->subtree_xor[$v];
$T2 = $total ^ $T1;
for ($w = 1; $w < $n; $w++) {
if ($w == $v) continue;
if ($this->in_time[$v] <= $this->in_time[$w] && $this->in_time[$w] <= $this->out_time[$v]) {
$comp1 = $this->subtree_xor[$w];
$comp2 = $T1 ^ $comp1;
$comp3 = $T2;
$max_val = max($comp1, $comp2, $comp3);
$min_val = min($comp1, $comp2, $comp3);
$score_candidate = $max_val - $min_val;
if ($score_candidate < $min_score) {
$min_score = $score_candidate;
}
}
}
for ($w = 1; $w < $n; $w++) {
if ($w == $v) continue;
if ($this->in_time[$v] <= $this->in_time[$w] && $this->in_time[$w] <= $this->out_time[$v]) {
continue;
}
if ($this->in_time[$w] <= $this->in_time[$v] && $this->in_time[$v] <= $this->out_time[$w]) {
$comp2 = $this->subtree_xor[$w] ^ $this->subtree_xor[$v];
} else {
$comp2 = $this->subtree_xor[$w];
}
$comp1 = $T1;
$comp3 = $T2 ^ $comp2;
$max_val = max($comp1, $comp2, $comp3);
$min_val = min($comp1, $comp2, $comp3);
$score_candidate = $max_val - $min_val;
if ($score_candidate < $min_score) {
$min_score = $score_candidate;
}
}
}
return $min_score;
}
/**
* @param $u
* @param $p
* @return void
*/
function dfs($u, $p) {
$this->parent[$u] = $p;
$this->in_time[$u] = $this->time++;
$this->subtree_xor[$u] = $this->nums[$u];
foreach ($this->graph[$u] as $v) {
if ($v == $p) continue;
$this->dfs($v, $u);
$this->subtree_xor[$u] ^= $this->subtree_xor[$v];
}
$this->out_time[$u] = $this->time - 1;
}
}
// Test cases
$sol = new Solution();
// Example 1
$nums = [1, 5, 5, 4, 11];
$edges = [[0,1],[1,2],[1,3],[3,4]];
echo "Output: " . $sol->minimumScore($nums, $edges) . "\n"; // Expected: 9
// Example 2
$nums = [5,5,2,4,4,2];
$edges = [[0,1],[1,2],[5,2],[4,3],[1,3]];
echo "Output: " . $sol->minimumScore($nums, $edges) . "\n"; // Expected: 0
?>Explanation:
This approach efficiently explores all possible pairs of edge removals by leveraging subtree properties and XOR operations, ensuring optimal performance for the given constraints. |
Beta Was this translation helpful? Give feedback.
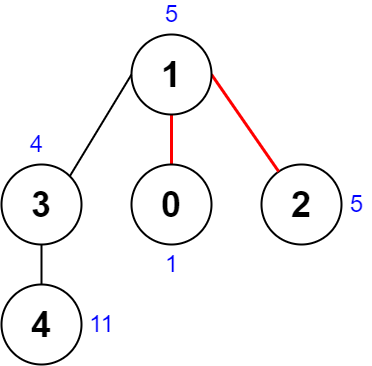
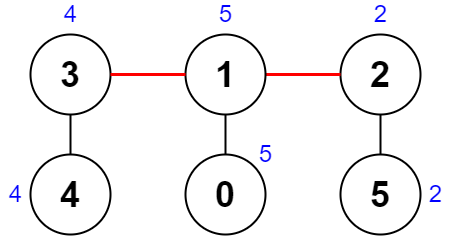
We need to find the minimum score after removing two distinct edges from a tree, resulting in three connected components. The score is defined as the difference between the largest and smallest XOR values of the three components.
Approach