2106. Maximum Fruits Harvested After at Most K Steps #2005
-
|
Topics: Fruits are available at some positions on an infinite x-axis. You are given a 2D integer array You are also given an integer Return the maximum total number of fruits you can harvest. Example 1:
Example 2:
Example 3:
Constraints:
Hint:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to maximize the number of fruits harvested by moving at most Approach
Let's implement this solution in PHP: 2106. Maximum Fruits Harvested After at Most K Steps <?php
/**
* @param Integer[][] $fruits
* @param Integer $startPos
* @param Integer $k
* @return Integer
*/
function maxTotalFruits($fruits, $startPos, $k) {
$n = count($fruits);
if ($n == 0) return 0;
$positions = array_column($fruits, 0);
$amounts = array_column($fruits, 1);
$prefix = [0];
for ($i = 0; $i < $n; $i++) {
$prefix[$i+1] = $prefix[$i] + $amounts[$i];
}
$j0 = -1;
$low = 0;
$high = $n - 1;
while ($low <= $high) {
$mid = intdiv($low + $high, 2);
if ($positions[$mid] <= $startPos) {
$j0 = $mid;
$low = $mid + 1;
} else {
$high = $mid - 1;
}
}
$j1 = -1;
$low = 0;
$high = $n - 1;
while ($low <= $high) {
$mid = intdiv($low + $high, 2);
if ($positions[$mid] >= $startPos) {
$j1 = $mid;
$high = $mid - 1;
} else {
$low = $mid + 1;
}
}
if ($j1 == -1) {
$j1 = $n;
}
$ans = 0;
if ($j0 >= 0) {
for ($i = 0; $i <= $j0; $i++) {
$steps = $startPos - $positions[$i];
if ($steps <= $k) {
$total = $prefix[$j0 + 1] - $prefix[$i];
if ($total > $ans) {
$ans = $total;
}
}
}
}
if ($j1 < $n) {
for ($i = $j1; $i < $n; $i++) {
$steps = $positions[$i] - $startPos;
if ($steps <= $k) {
$total = $prefix[$i + 1] - $prefix[$j1];
if ($total > $ans) {
$ans = $total;
}
}
}
}
if ($j0 >= 0) {
for ($i = 0; $i <= $j0; $i++) {
$max_r = $k - $startPos + 2 * $positions[$i];
if ($max_r < $startPos) {
continue;
}
$low_bound = 0;
$high_bound = $n - 1;
$r_index = -1;
$low = 0;
$high = $n - 1;
while ($low <= $high) {
$mid = intdiv($low + $high, 2);
if ($positions[$mid] <= $max_r) {
$r_index = $mid;
$low = $mid + 1;
} else {
$high = $mid - 1;
}
}
if ($r_index == -1) {
continue;
}
$total = $prefix[$r_index + 1] - $prefix[$i];
if ($total > $ans) {
$ans = $total;
}
}
}
if ($j1 < $n) {
for ($i = $j1; $i < $n; $i++) {
$min_l = 2 * $positions[$i] - $k - $startPos;
$low_bound = 0;
$high_bound = $i;
$l_index = -1;
$low = 0;
$high = $i;
while ($low <= $high) {
$mid = intdiv($low + $high, 2);
if ($positions[$mid] >= $min_l) {
$l_index = $mid;
$high = $mid - 1;
} else {
$low = $mid + 1;
}
}
if ($l_index == -1) {
continue;
}
$total = $prefix[$i + 1] - $prefix[$l_index];
if ($total > $ans) {
$ans = $total;
}
}
}
return $ans;
}
// Test cases
$fruits1 = [[2,8],[6,3],[8,6]];
echo maxTotalFruits($fruits1, 5, 4) . "\n"; // 9
$fruits2 = [[0,9],[4,1],[5,7],[6,2],[7,4],[10,9]];
echo maxTotalFruits($fruits2, 5, 4) . "\n"; // 14
$fruits3 = [[0,3],[6,4],[8,5]];
echo maxTotalFruits($fruits3, 3, 2) . "\n"; // 0
?>Explanation:
|
Beta Was this translation helpful? Give feedback.
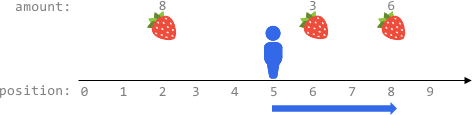
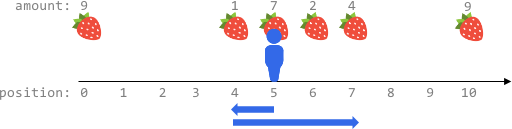
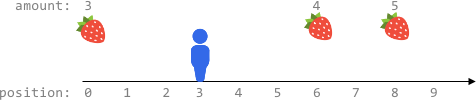
We need to maximize the number of fruits harvested by moving at most
ksteps from a starting position on an infinite x-axis. The fruits are located at specific positions, and we can move left or right, harvesting fruits at each position we visit. The solution involves considering different movement patterns to cover the maximum number of fruits within the step constraint.Approach
Problem Analysis: The problem requires us to find the optimal path that maximizes the fruit harvest while moving at most
ksteps. The fruits are given as a sorted list of positions and amounts. The key insight is that the optimal path can be one of four types: