3363. Find the Maximum Number of Fruits Collected #2022
-
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to maximize the number of fruits collected by three children moving through an Approach
Let's implement this solution in PHP: 3363. Find the Maximum Number of Fruits Collected <?php
/**
* @param Integer[][] $fruits
* @return Integer
*/
function maxCollectedFruits($fruits) {
$n = count($fruits);
$diagonalSum = 0;
for ($i = 0; $i < $n; $i++) {
$diagonalSum += $fruits[$i][$i];
}
$dp2_prev = array_fill(0, $n, -1);
$dp2_prev[$n-1] = $fruits[0][$n-1];
for ($k = 1; $k < $n; $k++) {
$dp2_curr = array_fill(0, $n, -1);
$minJ = max(0, $n-1 - $k);
$maxJ = min($n-1, $n-1 + $k);
for ($j = $minJ; $j <= $maxJ; $j++) {
$best = -1;
for ($d = -1; $d <= 1; $d++) {
$prevJ = $j + $d;
if ($prevJ >= 0 && $prevJ < $n && $dp2_prev[$prevJ] != -1) {
if ($best < $dp2_prev[$prevJ]) {
$best = $dp2_prev[$prevJ];
}
}
}
if ($best == -1) {
continue;
}
$add = ($j == $k) ? 0 : $fruits[$k][$j];
$dp2_curr[$j] = $best + $add;
}
$dp2_prev = $dp2_curr;
}
$totalSecond = $dp2_prev[$n-1] == -1 ? 0 : $dp2_prev[$n-1];
$dp3_prev = array_fill(0, $n, -1);
$dp3_prev[$n-1] = $fruits[$n-1][0];
for ($k = 1; $k < $n; $k++) {
$dp3_curr = array_fill(0, $n, -1);
$minI = max(0, $n-1 - $k);
$maxI = min($n-1, $n-1 + $k);
for ($i = $minI; $i <= $maxI; $i++) {
$best = -1;
for ($d = -1; $d <= 1; $d++) {
$prevI = $i + $d;
if ($prevI >= 0 && $prevI < $n && $dp3_prev[$prevI] != -1) {
if ($best < $dp3_prev[$prevI]) {
$best = $dp3_prev[$prevI];
}
}
}
if ($best == -1) {
continue;
}
$add = ($i == $k) ? 0 : $fruits[$i][$k];
$dp3_curr[$i] = $best + $add;
}
$dp3_prev = $dp3_curr;
}
$totalThird = $dp3_prev[$n-1] == -1 ? 0 : $dp3_prev[$n-1];
return $diagonalSum + $totalSecond + $totalThird;
}
// Test cases
$fruits = [[1,2,3,4],[5,6,8,7],[9,10,11,12],[13,14,15,16]];
echo maxCollectedFruits($fruits); // Output: 100
$fruits = [[1,1],[1,1]];
echo maxCollectedFruits($fruits); // Output: 4
?>Explanation:
This approach efficiently computes the maximum fruits collected by leveraging dynamic programming for the paths of Child 2 and Child 3, while Child 1's path is handled separately along the diagonal. The solution ensures optimal performance with a time complexity of O(n²), suitable for the given constraints. |
Beta Was this translation helpful? Give feedback.
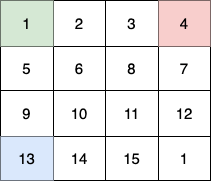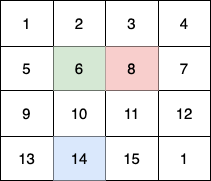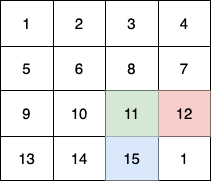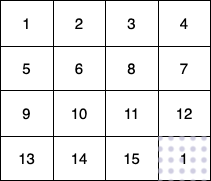
We need to maximize the number of fruits collected by three children moving through an
n x ngrid of rooms. Each child starts at a different corner of the grid and moves towards the bottom-right corner(n-1, n-1)in exactlyn-1moves, following specific movement rules. The challenge is to compute the maximum total fruits collected, considering that if multiple children visit the same room, the fruits in that room are counted only once.Approach
Problem Analysis:
n-1moves. Thus, Child 1's path is fixed:(0,0) → (1,1) → ... → (n-1, n-1). The fruits collected along this diagonal are s…