|
| 1 | + |
| 2 | +title: 说说SVG的feTurbulence滤镜 |
| 3 | +subtitle: 小目标:学学图形学,然后变成光 |
| 4 | +cover: https://img11.360buyimg.com/imagetools/jfs/t1/164343/5/19871/241244/607e6bf0Eb6fc9d06/21c8562e73c678d5.jpg |
| 5 | +tags: |
| 6 | + - 动画 |
| 7 | + - pc |
| 8 | + - 移动 |
| 9 | + - animation |
| 10 | +categories: Web开发 |
| 11 | +author: |
| 12 | + nick: yogurt |
| 13 | + github_name: yoturg |
| 14 | +date: 2021-04-20 13:49:04 |
| 15 | + |
| 16 | +--- |
| 17 | + |
| 18 | +很多时候,我们在布置游戏地图或者动漫场景的时候,需要模拟火焰,树丛,云朵等等这些大自然鬼斧神工创造出来的形状或者纹理,这个时候,你会发现这些形状整体看起来很有规律,但形状的延续却完全随机,乱中有序。 |
| 19 | + |
| 20 | +上个世纪80年代,***Ken Perlin*** 就思考过怎样模拟这些自然纹理这个问题,并且,给出了他的答案。在完全随机的白噪声函数上,用缓动曲线进行平滑插值,让函数的图像更加趋近于自然噪声的图像,也就是符合自然界形状和纹理规律的图像,由此发明了Perlin噪声算法。Perlin噪声算法提出后在很多场景都发挥了很大的作用,为迪士尼创造电影场景提供了许多帮助,曾经获得奥斯卡科技成果奖,是一个演技得到过认可的算法。 |
| 21 | + |
| 22 | +如今Perlin算法成了计算机图形学基础中的一员,任何跟图形学相关的工具库,都有他的实现,我们可以利用这些工具,从应用的角度学习Perlin噪声算法。 |
| 23 | + |
| 24 | +在SVG中,feTurbulence滤镜就可以利用Perlin函数创建丰富的图像。使用feTurbulence滤镜的时候,我们可以通过调整参数直观地看到效果,本文是对feTurbulence滤镜的学习记录,通过一些实验了解不同参数对feTurbulence滤镜创造出来的图像的影响。 |
| 25 | + |
| 26 | +## feTurbulence的参数 |
| 27 | + |
| 28 | +首先,通过[mdn](https://developer.mozilla.org/zh-CN/docs/Web/SVG/Element/feTurbulence) 我们可以初步了解一下feTurbulence滤镜的基本情况,他接收五个参数: |
| 29 | + |
| 30 | ++ baseFrequency(默认值:0) |
| 31 | ++ numOctaves(默认值:1) |
| 32 | ++ seed (默认值:0) |
| 33 | ++ stitchTiles(默认值:noStitch) |
| 34 | ++ type (默认值:turbulence) |
| 35 | + |
| 36 | +虽然不知道这五个参数有什么作用,但是既然feTurbulence所有参数都有默认值,那我们不入参地创造一个滤镜,然后一个参数一个参数探究一下,代码如下: |
| 37 | + |
| 38 | +```html |
| 39 | +<svg width="500" height="500"> |
| 40 | + <!-- 定义一个滤镜预设组 --> |
| 41 | + <filter id='noise'> |
| 42 | + <!-- 向组中添加主角 --> |
| 43 | + <feTurbulence/> |
| 44 | + </filter> |
| 45 | + <!-- 创建一个矩形,把滤镜效果应用到矩形上 --> |
| 46 | + <rect width="100%" height="100%" filter="url(#noise)" fill="none"> |
| 47 | +</svg> |
| 48 | +``` |
| 49 | + |
| 50 | +### baseFrequency |
| 51 | + |
| 52 | +把上面的代码放入页面运行,我们什么东西都看不到,因为baseFrequency在不入参的情况默认值为0。而baseFrequency影响的是噪声的频率,当噪声的频率为0时,就自然没有图像啦。 |
| 53 | + |
| 54 | +频率越大,相同显示区域下可以显示的噪声就越密集,当baseFrequency的值为一个很小的值时(如0.01),生成的图像比较大,细节更丰富,而增大10倍之后,原来的图像被缩小10倍放到左上角,剩余的空间用来放置更多的噪声 |
| 55 | + |
| 56 | +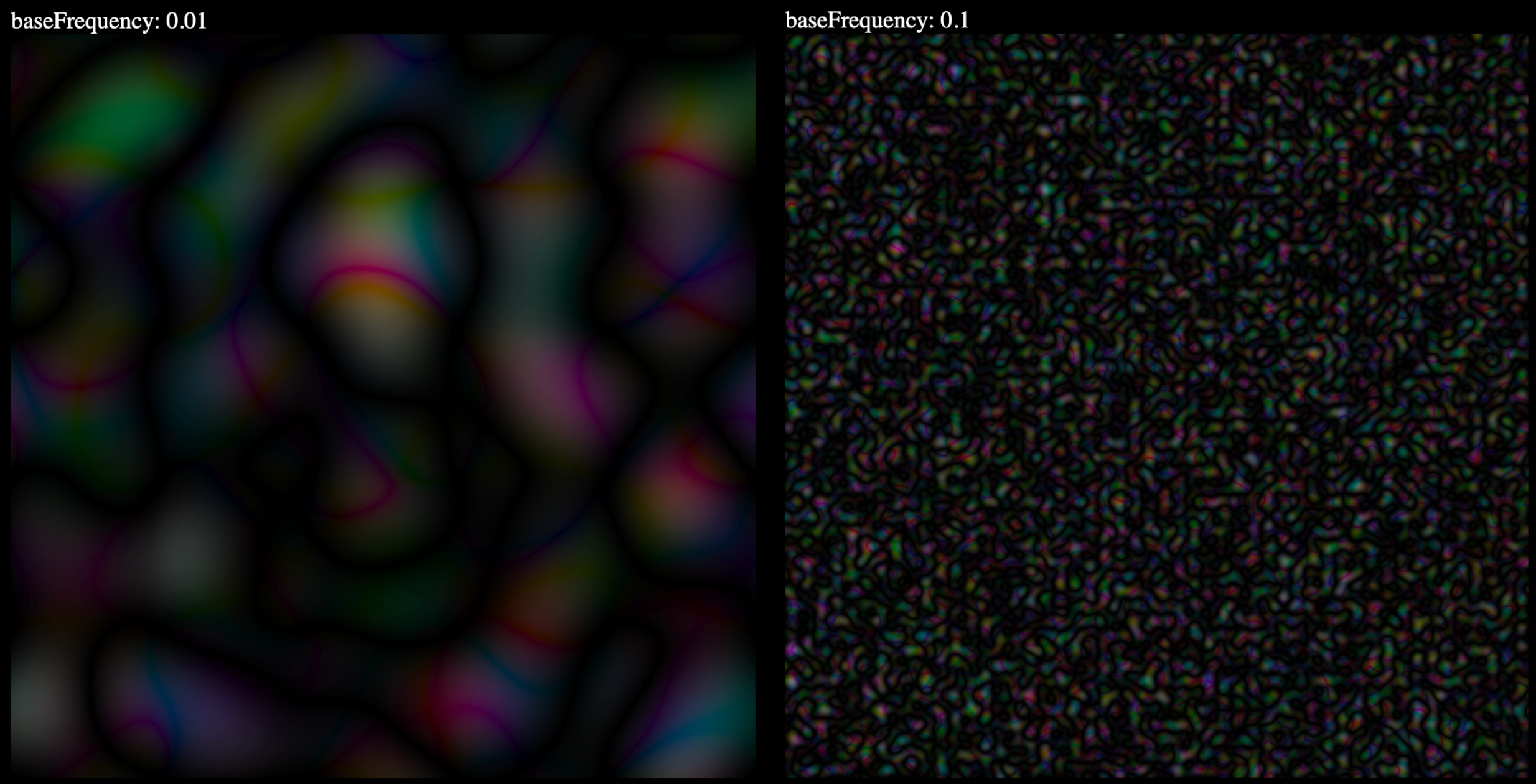 |
| 57 | + |
| 58 | +以下是baseFrequency的值慢慢变大的过程 |
| 59 | + |
| 60 | + |
| 61 | + |
| 62 | +baseFrequency属性可以接受两个值,当这样入参的时候,这两个值分别会当成x轴和y轴上的基础频率,由此,我们可以生成在某一个方向拉伸的噪声。 |
| 63 | + |
| 64 | + |
| 65 | + |
| 66 | +### numOctaves |
| 67 | + |
| 68 | +octaves是八度的意思,玩过音乐的同学都知道,两个相邻音组中的同名音之间的音高差距就是一个八度,这两个音振动图像相似,高八度的音的振动频率刚好是低八度的两倍。相差八度的两个音同时弹响的时候,可以产生细节更加丰富的音。 |
| 69 | + |
| 70 | +在数学函数里,一个函数跟他另一个不同频率的函数叠加,也可以达到一样的效果,产生一个轮廓不变,细节更加丰富的函数图像。 |
| 71 | + |
| 72 | +我们以sin函数为例,以下是f(x) = sin(x)和f(x) = sin(10x)的函数图像: |
| 73 | + |
| 74 | +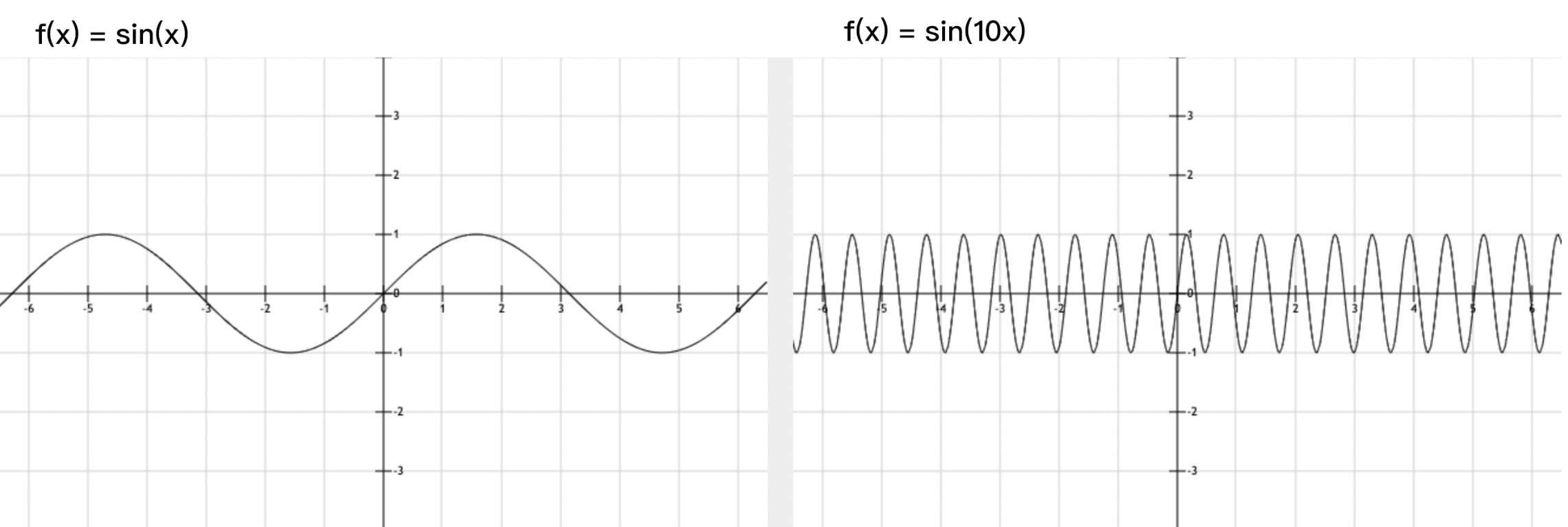 |
| 75 | + |
| 76 | +两个图象的振幅一样,后者的频率是前者的10倍,高了10个八度,现在让两个函数同时弹响,形成: |
| 77 | + |
| 78 | +``` |
| 79 | +f(x) = sin(x) + sin(10) |
| 80 | +``` |
| 81 | + |
| 82 | +他的图像会是怎么样的呢? |
| 83 | + |
| 84 | +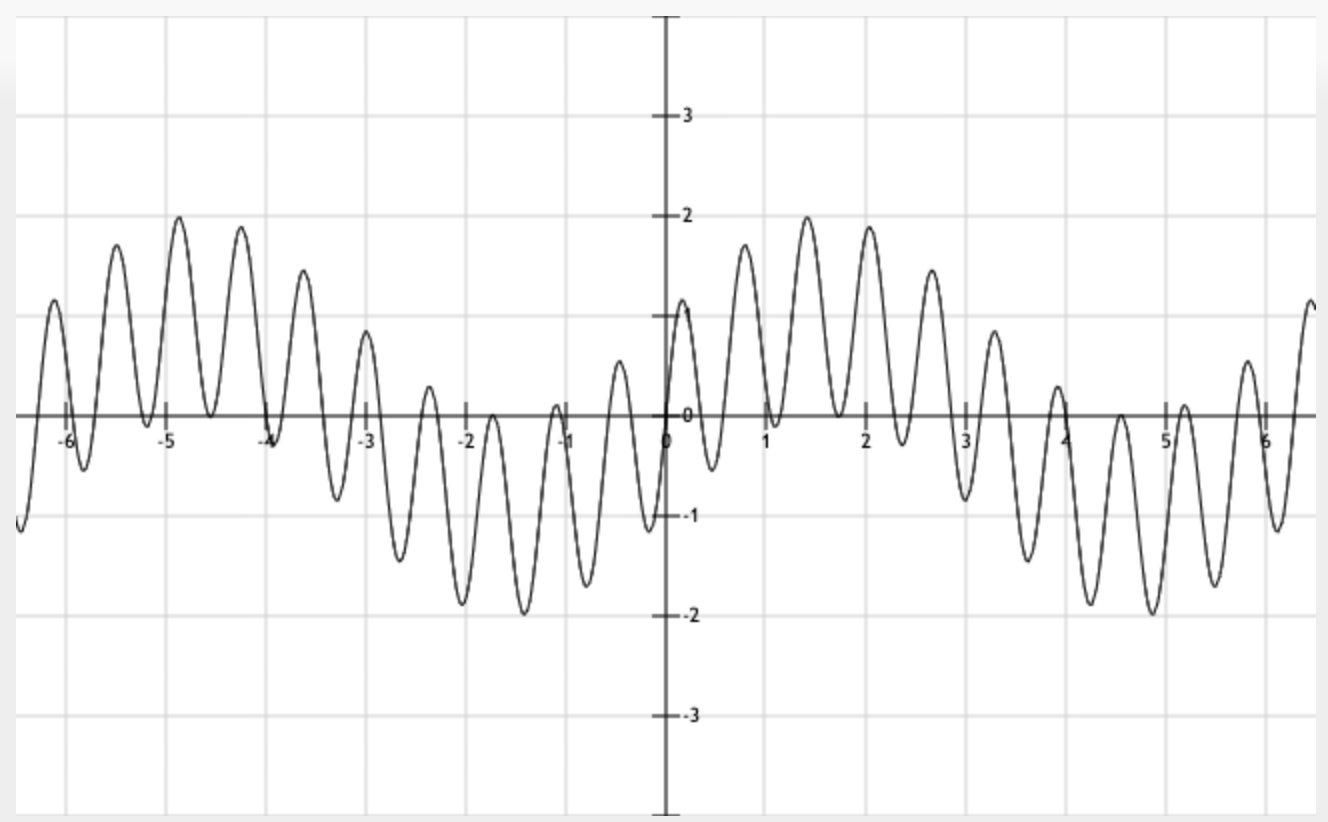 |
| 85 | + |
| 86 | +对比前面三个图像,第三个图像感觉就像是拿第二个图像当画笔画出来的第一个图像。这,就是八度和弦的魅力,我还是原来的我,然而我花里胡哨起来了。如果再花里胡哨一点,在第三个函数上叠多一个高10个八度的函数,会不会更快乐呢。 |
| 87 | + |
| 88 | +``` |
| 89 | +f(x) = sin(x) + sin(10x) + sin(20x) |
| 90 | +``` |
| 91 | + |
| 92 | +说回numOctaves属性,当我们设置了这个属性之后,算法会在原来的噪声函数上叠加若干个频率不同的他自己,形成细节更加丰富的噪声,看一下numOctaves增加时的动态效果。(这里说一下,numOctaves只接受不等于0的正整数,这是因为八度叠加的最小单位是一个八度,如果一个函数跟自己非整数倍频率的函数叠加,最终函数的大致形状会受到影响。) |
| 93 | + |
| 94 | + |
| 95 | + |
| 96 | +跟sin函数叠加自己的八度函数的效果一样,随着numOctaues不断增加,图像的大致形状还是跟numOctaues等于1的时候一样,但是细节在不断增加。有一个值得注意的点是,当numOctaues大于6之后,图像的区别开始变得不明显,这并不是到达某个阈值之后,八度叠加就不生效了,而是叠加之后产生的变化更加细小,需要拿个显微镜看一看啦。 |
| 97 | + |
| 98 | +### type |
| 99 | + |
| 100 | +feTurbulence的type属性把位于同一个子集的两个功能合并在一个滤镜里,type的取值是turbulence和fractalNoise。turbulence是指将柏林函数进行合成时,只取函数的绝对值,合成后的函数在0处不可导,其图像会有一些尖锐效果,形似湍流。fractalNoise则是在原来的噪声中叠加白噪声,让最终的结果呈现出高斯模糊的效果。两种type对应的原理大家可以自行百度谷歌。简单来说两个的区别是有没有模糊。 |
| 101 | + |
| 102 | +以下是两种type的效果 |
| 103 | + |
| 104 | + |
| 105 | + |
| 106 | +### stitchTiles |
| 107 | + |
| 108 | +stitchTiles需要使用多个图形时才能发挥效果,当我们随便设置两个使用feTurbulence滤镜的图形放在一起的时候,这两个图形的边界会出来断层的现象。两个图形就是独立的个体,自己顾自己长什么样。 |
| 109 | + |
| 110 | +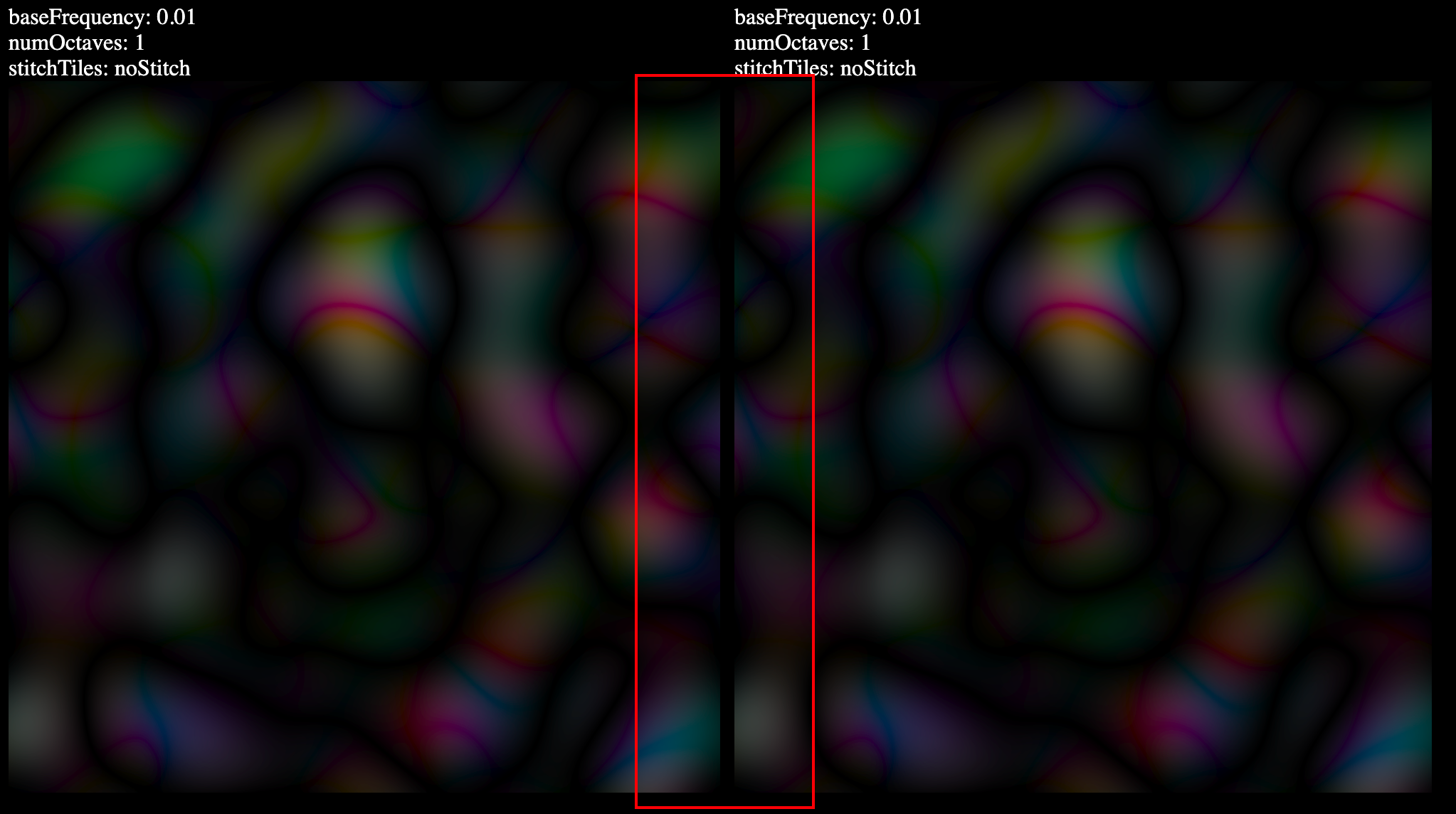 |
| 111 | + |
| 112 | +但是有时候,我们需要让两个图形看起来像从一个连续的集合分开。这个时候就可以将滤镜的stitchTiles属性设置成stitch,那这个时候,图形的边界就会连续起来。 |
| 113 | + |
| 114 | +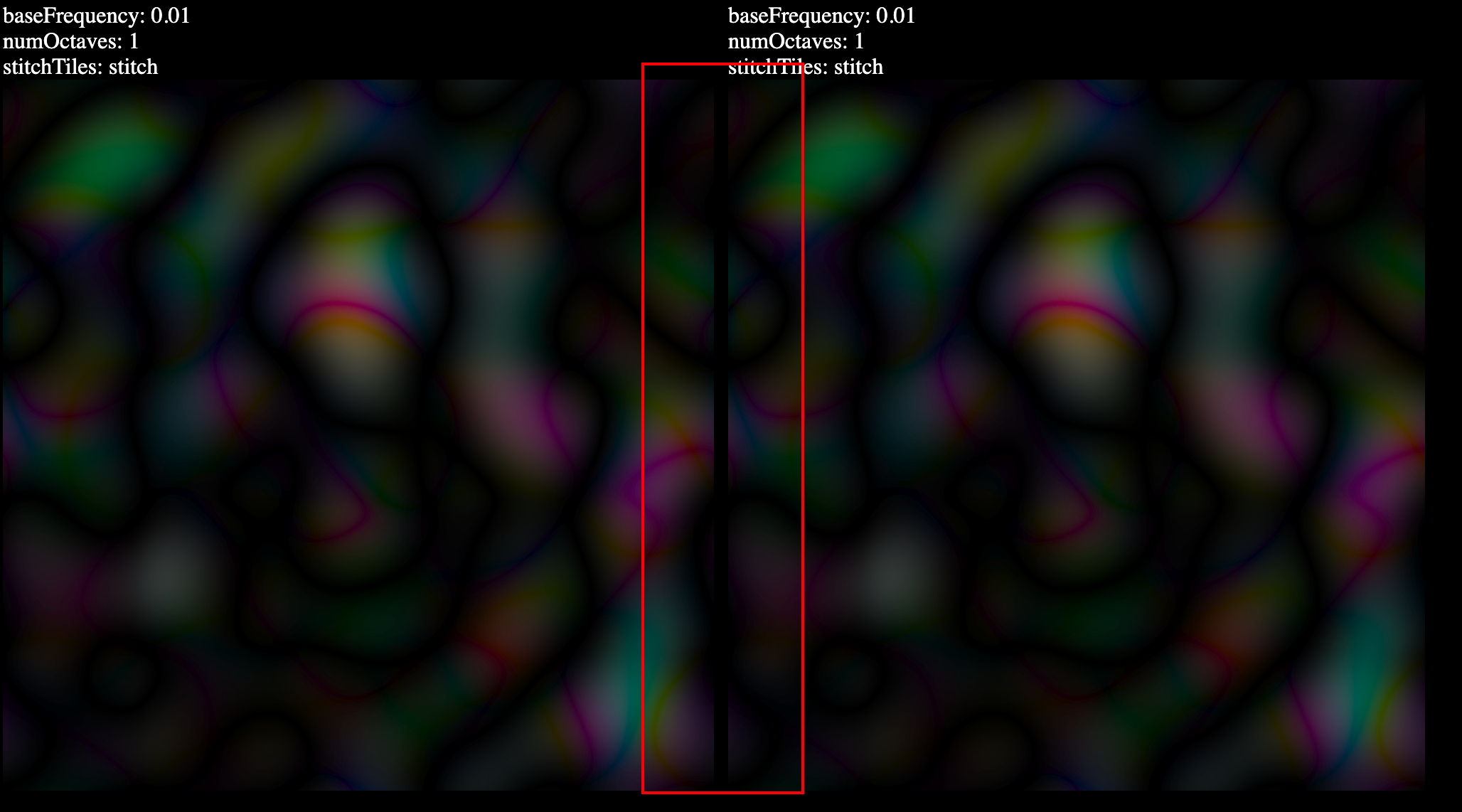 |
| 115 | + |
| 116 | +### seed |
| 117 | + |
| 118 | +seed是种子的意思,这是每一个随机数算法都那需要用到的一个输入,所有的伪随机数算法中,当输入的种子一样的时候,输出总是一致的。 |
| 119 | + |
| 120 | + |
| 121 | + |
| 122 | +## feTurbulence的使用 |
| 123 | + |
| 124 | +从上文一路到这里,沿路上已经出现了很多feTurbulence滤镜创造的图像,有静止的、动态、密集的、拉伸的。可能这些图像让人觉得很陌生,但这些确实都是日常生活中会出现的图像。老电视在播放画面的时候,会受到电磁波的影响,偶尔出现一扫而过的扭曲画面;牛皮纸粗糙的表面在光线下,会表现出特有的纹理......当我们想去表达一个受自然噪声影响的事物的时候,都可以使用feTurbulence滤镜,再结合光线,图片,色块等元素进行描述。 |
| 125 | + |
| 126 | +### 水流纹路 |
| 127 | + |
| 128 | +当河水平缓流动的时候,水面会出现很多细小的波纹,这种纹路符合的水平拉伸的图像特点,我们可以创建一个图像,再添加一点动效 |
| 129 | + |
| 130 | +```svg |
| 131 | +<filter id='turbulence-noise' x='0%' y='0%' width='100%' height='100%'> |
| 132 | + <feTurbulence id="feturbulence" baseFrequency="0.015 0.3"> |
| 133 | + <animate id="ani1" attributeName="baseFrequency" dur="15s" from="0.015 0.3" to="0.035 0.5" begin="0s; ani2.end" |
| 134 | + fill="feeze"> |
| 135 | + </animate> |
| 136 | + |
| 137 | + <animate id="ani2" attributeName="baseFrequency" dur="15s" from="0.035 0.5" to="0.015 0.3" begin="ani1.end" |
| 138 | + fill="freeze"> |
| 139 | + </animate> |
| 140 | + </feTurbulence> |
| 141 | +</filter> |
| 142 | +``` |
| 143 | + |
| 144 | +运行代码我们可以看到这样的效果: |
| 145 | + |
| 146 | + |
| 147 | + |
| 148 | +在这个效果的基础上,使用feDisplacementMap滤镜把一张静态的河流图片映射到图像上,就可以看到以下的效果。此处参考了[网上大佬的作品](https://wow.techbrood.com/fiddle/30865),有兴趣可以看看源代码。 |
| 149 | + |
| 150 | + |
| 151 | + |
| 152 | +### 纸张的纹路 |
| 153 | + |
| 154 | +相比于水流的纹路,纸张的纹路更加密集,图像细节更加丰富,而且纹路的线条界线不明显。根据这个特点,我们可以把feTurbulence的参数设置成 |
| 155 | + |
| 156 | +```svg |
| 157 | +<feTurbulence type="fractalNoise" baseFrequency='0.04' result='noise' numOctaves="5" /> |
| 158 | +``` |
| 159 | + |
| 160 | +得到这样的图像 |
| 161 | + |
| 162 | +然后,使用白光从图像上方45度角进行照射,得到以下图形 |
| 163 | + |
| 164 | + |
| 165 | + |
| 166 | + |
| 167 | + |
| 168 | +## 总结 |
| 169 | + |
| 170 | +feTurbulence实现了Perlin噪声算法,因此我们可以拿他来模拟绝大部分自然形成的图像,这是一个具有很高可玩性的滤镜,只要我们了解光影变化的原理,从数学的角度认识世界,就可以找到很多可以跟feTurbulence滤镜结合的元素,创造更多意想不到的玩法。 |
| 171 | + |
| 172 | + |
| 173 | + |
| 174 | + |
| 175 | + |
| 176 | +## 参考 |
| 177 | + |
| 178 | +[流水的动效](https://wow.techbrood.com/fiddle/30865) |
| 179 | + |
| 180 | +[【计算机图形】Perlin Noise 实例和理解](https://blog.csdn.net/Sengo_GWU/article/details/80153638?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-7.control&dist_request_id=&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-7.control) |
| 181 | + |
| 182 | +[【图形学】谈谈噪声](https://blog.csdn.net/weixin_34342905/article/details/93813626) |
| 183 | + |
| 184 | +[SVG Filter Effects: Creating Texture with <feTurbulence>](https://tympanus.net/codrops/2019/02/19/svg-filter-effects-creating-texture-with-feturbulence/) |
| 185 | + |
0 commit comments