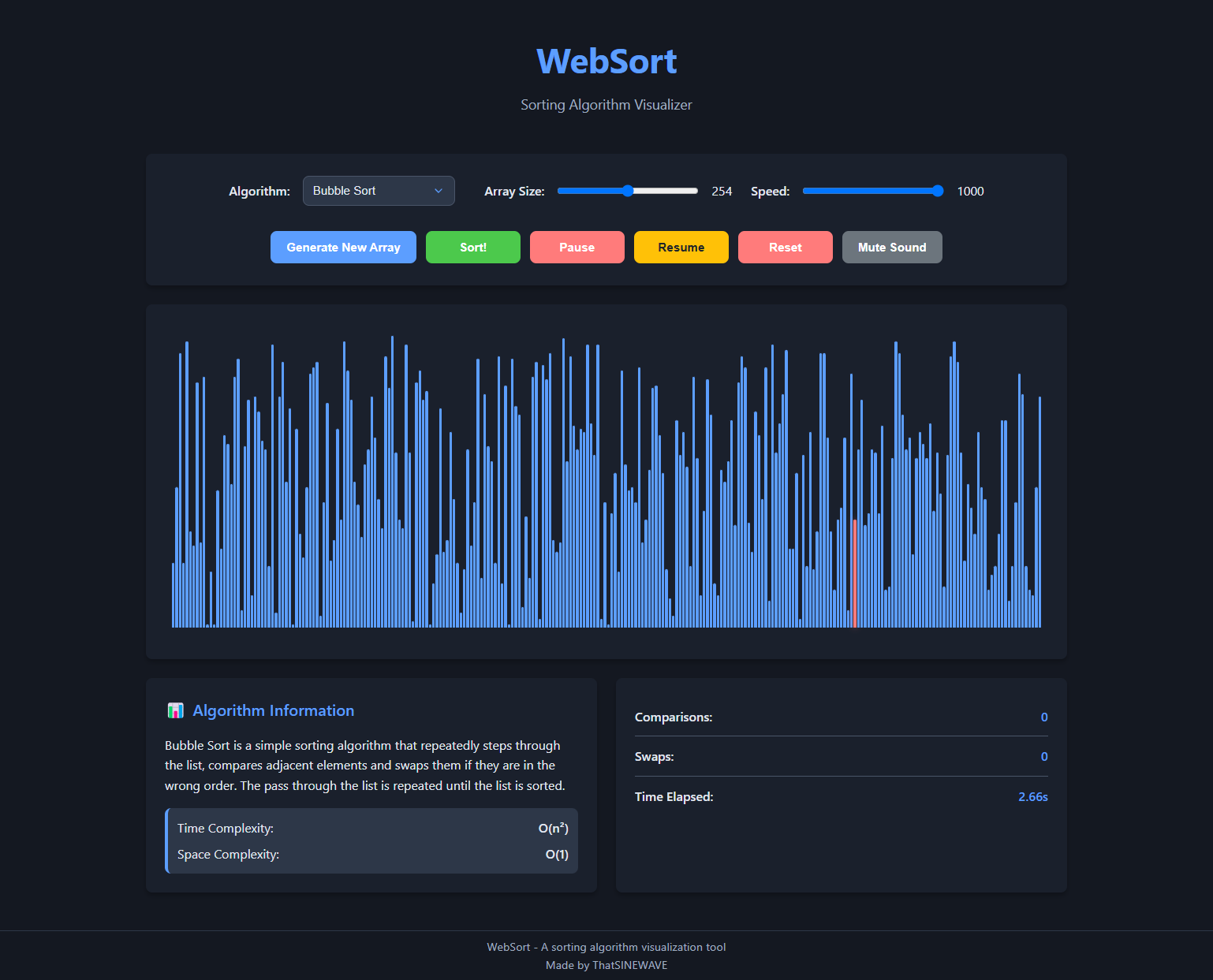
WebSort is an interactive web-based sorting algorithm visualizer that allows users to observe and compare various sorting algorithms in real-time. The project provides a visual and auditory representation of how different sorting algorithms manipulate data, making it easier to understand their behavior, efficiency, and performance characteristics.
- Visual Representation: See sorting algorithms in action with dynamic bar visualization
- Audio Feedback: Hear the sorting process with pitch changes based on swap frequency
- Real-time Statistics: Track comparisons, swaps, and elapsed time
- Interactive Controls:
- Adjust array size (10-500 elements)
- Control visualization speed
- Pause, resume, and reset sorting operations
- Generate new random arrays
- Algorithm Information: View detailed descriptions and complexity analyses
- Responsive Design: Works across desktop and mobile devices
- Dark Mode Support: Automatically switches based on system preferences
WebSort includes implementations of the following sorting algorithms:
A simple comparison-based algorithm that repeatedly steps through the list, compares adjacent elements, and swaps them if they're in the wrong order. Not suitable for large datasets.
- Time Complexity: O(n²)
- Space Complexity: O(1)
Builds the sorted array one item at a time by repeatedly taking the next unsorted item and inserting it into its correct position. Efficient for small datasets and nearly sorted arrays.
- Time Complexity: O(n²)
- Space Complexity: O(1)
Repeatedly finds the minimum element from the unsorted portion of the array and moves it to the beginning of the unsorted portion. Simple but inefficient for large lists.
- Time Complexity: O(n²)
- Space Complexity: O(1)
A divide-and-conquer algorithm that divides the input array into two halves, recursively sorts them, and then merges the sorted halves. Efficient and stable.
- Time Complexity: O(n log n)
- Space Complexity: O(n)
Another divide-and-conquer algorithm that selects a 'pivot' element and partitions the array around it. Highly efficient for large datasets but can degrade to O(n²) in worst cases.
- Time Complexity: O(n²) worst case, O(n log n) average
- Space Complexity: O(log n)
Builds a max heap from the array and then repeatedly extracts the maximum element. Efficient and in-place but not stable.
- Time Complexity: O(n log n)
- Space Complexity: O(1)
An optimization of insertion sort that allows the exchange of items that are far apart. More efficient than insertion sort for larger lists.
- Time Complexity: O(n(log n)²) (depends on gap sequence)
- Space Complexity: O(1)
A non-comparison-based algorithm that works by counting the occurrences of each unique element in the array. Efficient for arrays with a small range of values.
- Time Complexity: O(n + k) where k is the range
- Space Complexity: O(k)
A non-comparative sorting algorithm that sorts integers by processing individual digits. Efficient for integers with a fixed number of digits.
- Time Complexity: O(nk) where k is the number of digits
- Space Complexity: O(n + k)
A variation of bubble sort that sorts in both directions, potentially reducing the number of iterations needed.
- Time Complexity: O(n²)
- Space Complexity: O(1)
Similar to insertion sort but moving elements one at a time and going back if necessary. Simple but inefficient.
- Time Complexity: O(n²)
- Space Complexity: O(1)
A highly inefficient sorting algorithm based on random permutation of the array. Included as an educational example of how not to sort.
- Time Complexity: O(n × n!) (unbounded)
- Space Complexity: O(1)
An in-place, unstable sorting algorithm that minimizes memory writes. Optimal for minimizing writes but slow for general use.
- Time Complexity: O(n²)
- Space Complexity: O(1)
An improvement over bubble sort that uses a shrinking gap sequence. More efficient than bubble sort for random arrays.
- Time Complexity: O(n²) worst case, O(n log n) average
- Space Complexity: O(1)
A sorting algorithm that sorts by repeatedly flipping the largest unsorted element to the beginning, then flipping it back to its correct position.
- Time Complexity: O(n²)
- Space Complexity: O(1)
A recursive sorting algorithm that divides the array into thirds. Highly inefficient but interesting for educational purposes.
- Time Complexity: O(n^(log 3/log 1.5)) ≈ O(n^2.7095)
- Space Complexity: O(log n) due to recursion
A parallel sorting algorithm based on the bitonic sequence concept. Performs well in parallel processing environments.
- Time Complexity: O(log² n)
- Space Complexity: O(n log² n) in parallel, O(1) in place
Also known as Brick Sort, this algorithm is a variation of bubble sort that works by comparing all odd/even indexed pairs of adjacent elements and swapping them if needed. It's simple to implement in parallel architectures.
- Time Complexity: O(n²)
- Space Complexity: O(1)
A hybrid stable sorting algorithm derived from merge sort and insertion sort, designed to perform well on many kinds of real-world data. It's the default sorting algorithm in Python, Java, and many other programming languages.
- Time Complexity: O(n log n)
- Space Complexity: O(n)
A sorting algorithm suitable for sorting lists of elements where the number of elements and the range of possible key values are approximately the same. It works by creating "pigeonholes" for each possible value and distributing elements into them.
- Time Complexity: O(n + range) where range is the range of input values
- Space Complexity: O(range)
Also known as Gravity Sort, this is a natural sorting algorithm inspired by beads falling under gravity. It's primarily suitable for non-negative integers and works by representing each number as a stack of beads.
- Time Complexity: O(n²) in general, O(n) on some hardware
- Space Complexity: O(n × max) where max is the maximum element
A distribution sort that works by distributing elements into a number of buckets, then sorting each bucket individually (usually with another algorithm). Efficient when input is uniformly distributed across a range.
- Time Complexity: O(n²) worst case, O(n + k) average where k is the number of buckets
- Space Complexity: O(n + k)
-
Clone the repository:
git clone https://github.com/ThatSINEWAVE/WebSort.git
-
Navigate to the project directory:
cd WebSort -
Open
index.htmlin your browser, or use a local server:# Using Python 3 python -m http.server -
Access the application at
http://localhost:8000
- Select a sorting algorithm from the dropdown menu
- Adjust the array size and sorting speed as desired
- Click "Generate New Array" to create a random data set
- Click "Sort!" to start the visualization
- Use the Pause/Resume/Reset buttons to control the process
- Algorithm implementations based on established computer science principles
- Design inspired by modern web development practices
Feel free to submit issues or contribute improvements via pull requests.
This project is open-source and available under the MIT License.