跳表是一种允许以O(logn)时间复杂度进行查询和插入的数据结构,它相比与红黑树或者平衡树来说实现更加简单。
假设一个单链表结构,即使是有序的,要查询某个元素时,也只能进行遍历查询,即时间复杂度为O(n)(即使,采用双向链表,其时间复杂度也是O(N))。
因此如何提高链表的检索效率?
// todo 以后争取更换成 ipad 画图。
依次类推,当层高为K时,在合适的散列情况下,最坏时间复杂度是
O(k*(n)^(1/n))
特殊情况,当 k=logN 时,时间复杂度为:
T=logN*(n^(1/logN)) = logN*(2^(1/logN*logN)) = logN
由上面可以看到,当MaxLevel=16时,可以容纳的数据为 2^16 次方
因此,跳表的关键在于元素变更后,如何维护高效的存储结构。
严格数学推导见skip_list_math
这里参考 redis 的源码来定义跳表的数据结构。
// 单个节点
typedef struct skip_list_node
{
// the value
Element e;
// the backward in the same level
struct skip_list_node *backward;
struct skip_list_level
{
// the next node in the same level
struct skip_list_node *forward;
} level[];
} SkipListNode;
// 跳表 这里存储 header 和 tail 是为了方便前后遍历
typedef struct skip_list
{
SkipListNode *header, *tail;
// the size stored in this list
unsigned int size;
// the current maxt level
int level;
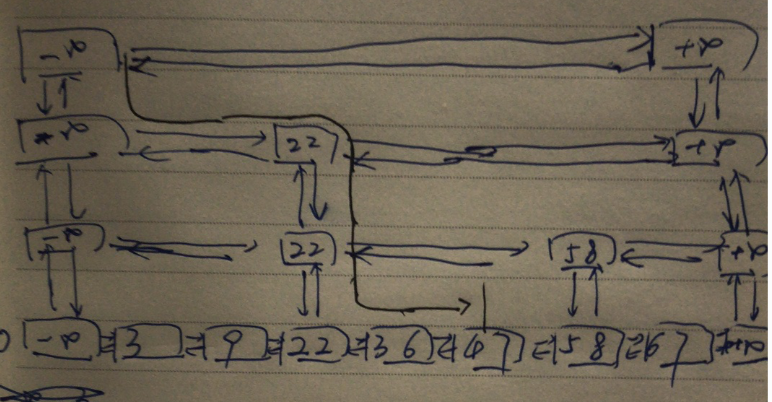
} SkipList;如上图,想要查询出47这个元素所在的节点,其查询路线如曲线所示。
查询过程如下:
从某一层链表某个的元素向后遍历,若刚好存在一个节点的值等于
A,则返回该节点,查询完成。否则,取最后一个值小于A的节点C,如果C已处于底层,则返回空,查询结束(此时未查询到)。若C还有更低层,向下一层遍历重复该步骤。
代码实现如下:
SkipListNode *skip_list_search(SkipList *list, Element e, compare_func cmp)
{
if (list->size == 0)
return NULL;
int level = list->level;
SkipListNode *head = list->header;
while (head && level >= 0)
{
SkipListNode *temp = head->level[level].forward;
if (temp == NULL)
{
level--;
}
else
{
int p = cmp(temp->e, e);
if (p == 0)
{
return temp;
}
else if (p < 0)
{
head = temp;
}
else
{
level--;
}
}
}
return NULL;
}根据上面的数学证明,我们知道了每次插入节点的level是随机的,因此采取随机数生成.
int random_level()
{
int level = 0;
while ((random() & 0xFFFF) < (SKIP_LIST_P * 0xFFFF))
{
level++;
}
return level < MAX_SKIP_LIST_LEVEL ? level : MAX_SKIP_LIST_LEVEL;
}void skip_list_insert(SkipList *list, Element e, compare_func cmp)
{
SkipListNode *update[MAX_SKIP_LIST_LEVEL], *x;
SkipListNode *head = list->header;
int i, level;
for (i = list->level; i >= 0; i--)
{
SkipListNode *temp = head->level[i].forward;
if (temp)
{
int p = cmp(temp->e, e);
// has exists return
if (p == 0)
return;
// if the value less target;node forward
// meantime,the left node update
else if (p < 0)
{
head = temp;
}
// if the value greater target; update the right node
// else continue;
}
update[i] = head;
}
// start modify the list
// meantime update the
level = random_level();
if (level > list->level)
{
for (i = list->level; i < level; i++)
{
update[i] = list->header;
}
list->level = level;
}
x = skip_list_node_new(e, level);
for (i = 0; i < level; i++)
{
x->level[i].forward = update[i]->level[i].forward;
update[i]->level[i].forward = x;
}
x->backward = (update[0] == list->header) ? NULL : update[0];
if (x->level[0].forward)
{
x->level[0].forward->backward = x;
}
else
{
list->tail = x;
}
list->size++;
return;
}delete 是相对较为简单的,只需要注意删除完节点之后,要查看高层次是否为空,及时删除。
void skip_list_delete(SkipList *list, Element e, compare_func cmp)
{
SkipListNode *update[MAX_SKIP_LIST_LEVEL], *x;
x = list->header;
int i, level;
for (i = list->level; i >= 0; i--)
{
while (x->level[i].forward && cmp(x->level[i].forward->e, e) < 0)
{
x = x->level[i].forward;
}
update[i] = x;
}
x = x->level[0].forward;
if (x && cmp(x->backward, e) == 0)
{
skip_list_delete_node(list, x, update);
free(x);
}
}
void skip_list_delete_node(SkipList *list, SkipListNode *node, SkipListNode **update)
{
int i;
for (i = 0; i < list->level; i++)
{
if (update[i]->level[i].forward == node)
{
update[i]->level[i].forward = node->level[i].forward;
}
}
if (node->level[0].forward)
{
node->level[0].forward->backward = node->backward;
}
else
{
list->tail = node->backward;
}
while (list->level > 0 && list->header->level[list->level].forward == NULL)
{
list->level--;
}
list->size--;
}